一名财务分析师想调查与大学生拥有特定信用卡的概率相关联的因子。分析师随机抽取了一些大学生进行调查。在调查中,学生将回答有关其教育和财务情况的问题。
出于市场营销目的,分析师希望确定与最不可能拥有 Master 卡的学生群体和最可能拥有 American Express 卡的学生群体相关的预测变量值。分析师对 American Express 卡和 Master 卡拟合二项 Logistic 回归模型,以确定预测变量如何与拥有其中每种信用卡的概率相关联。
在拟合模型之后,分析人员使用响应优化器查找为两种信用卡生成可接受概率的预测变量设置。
- 打开样本数据 信用卡调查.MWX.
- 选择。
- 在MasterCard行的目的中,选择最小化。
- 在American Express行的目的中,选择最大化。
- 单击确定。
解释结果
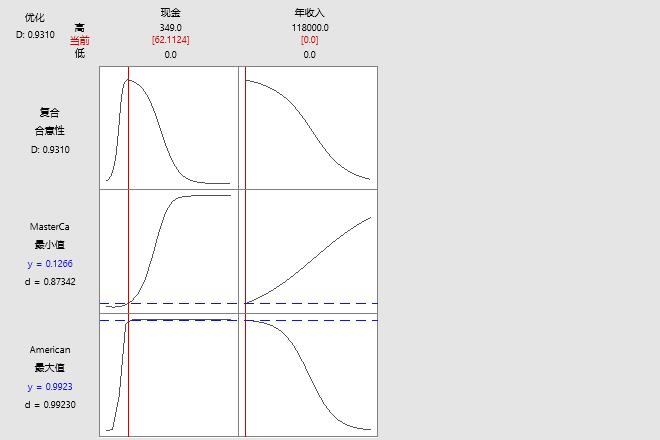
Minitab 使用两个存储模型估计对这两个响应变量的值进行优化的预测变量设置。这两个响应的合并合意性(又称为复合合意性)是 0.9310,这表明所得到的解非常优秀但还不够完美。
图形中显示的预测变量设置与拥有 MasterCard 信用卡的概率低但拥有 American Express 卡的概率高的学生相关联。这个学生总体的平均现金金额为 62.11 美元,他们没有年收入。输出结果指示这些值的拟合概率为 0.127(对于 Master Card)和 0.9923(对于 American Express)。置信区间指示这些预测的精确度。
可以直接在图上调整此初始解的变量设置。移动竖条以更改因子设置,并观察响应的单个合意性 (d) 以及复合合意性如何变化。
参数
| 响应 | 目的 | 下限 | 目标 | 上限 | 权重 | 重要度 |
|---|---|---|---|---|---|---|
| MasterCard | 最小值 | 0 | 1 | 1 | 1 | |
| American Express | 最大值 | 0 | 1 | 1 | 1 |
解
| 解 | 现金 | 年收入 | MasterCard 拟合概率 | American Express 拟合概率 | 复合合意性 |
|---|---|---|---|---|---|
| 1 | 62.1123 | 0 | 0.126577 | 0.992297 | 0.930964 |
多响应预测
| 变量 | 设置 |
|---|---|
| 现金 | 62.1123 |
| 年收入 | 0 |
| 响应 | 拟合概率 | 拟合值标准误 | 95% 置信区间 |
|---|---|---|---|
| MasterCard | 0.127 | 0.172 | (0.007, 0.754) |
| American Express | 0.9923 | 0.0322 | (0.0323, 1.0000) |
