多重配对比较的分组信息表
Minitab 使用两个水平均值之差的置信区间结果,获取分组信息。分组信息在矩阵中提供。假定一个项具有 k 个水平,则矩阵的最大尺寸为 k x k。如果所有水平均在一个组中,则尺寸为 k x 1,所有因子水平均具有字母“A”。如果所有水平处于不同的组中,尺寸为 k x k,仅具有对角字母。
- 对处于不同水平的所有最小二乘均值,按降序排序,表示为 1, 2, ... , k。
- 在每个单元格里,用值 0 定义 k x k 矩阵,其中 k = 因子水平数。
- 对于 j 列,其中 j = 1, ... ,Minitab 采取下列算法:
- 查看均值 j – 均值 r 的置信区间,其中 r = j + 1, .. , k。如果 r 的区间包含 0,则将第 r 行和第 j 列单元格 j) 设置为 1。
- 如果列 j 中至少有一个单元格具有值 1,则将 (j, j) 单元格设置为 1。
- 对于行 I = j + 1, ... , k,计算从列 1 到列 j 的行和。如果最小值(所有行和)>= 1,则终止循环;否则,执行 j + 1,然后转到步骤 a。
- 对于每个行 i,Minitab 将检查行 ≥ 1 的所有列值的和。如果和为 0,则设置行 i 和列 j 单元格 = 1,其中列 j 是具有值 0 的矩阵中的第一列。此过程将生成一个具有值 1 和 0 的矩阵。组的总数是非零列数。
- Minitab 会将字母匹配到列(例如 A 匹配列 1,B 匹配列 2,等等),并向具有值 1 的单元格分配正确的字母。
带控制的多重比较的分组信息表
Minitab 使用每个水平均值和控制水平之差的置信区间结果,获取分组信息。分组信息是带有一个列的矩阵。
Minitab 向控制水平分配了字母“A”。
如果区间包含 0,则水平均值与控制水平处于相同的组。Minitab 将向水平均值分配字母“A”。
如果区间不包含 0,则不会分配字母。
Tukey 法
公式
Tukey 法适用于所有的配对比较。置信区间公式如下所示:
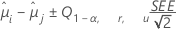
检验统计量的公式为:

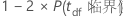
有关计算调整的 p 值的详细信息,请参见以下参考资料。
要从整体误差率中查找个别误差率,请使用以下公式:
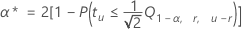
表示法
| 项 | 说明 |
|---|---|
 | 第 i 个因子水平或因子水平组合的最小二乘平均值 |
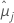 | 第 j 个因子水平或因子水平组合的最小二乘平均值 |
| r | 均值个数 |
| Q1 − α, r, u | 要与 u 个自由度进行比较的 r 均值的学生化极差分布的 1 − α 百分位数 |
| u | 模型的误差的自由度 |
| SEE | 最小二乘平均值之间估计差值的标准误 |
| α | 产生类型 I 错误的整体概率,基于学生化极差分布 |
| α* | 产生类型 I 错误的单个概率,基于一个比较的 t 分布 |
参考资料
1 Braun, H. I.,编辑 (1994),The collected works of John W. Tukey: Volume VIII Multiple comparisons 1948-1983(John W. Tukey 著作集:第八卷多重比较 1948-1983)。纽约:Chapman and Hall。
2 J.C. Hsu (1996),Multiple Comparisons: Theory and methods(多重比较:理论和方法),Chapman & Hall。
Fisher 法
公式
Minitab 为比较处理均值提供了不同的置信区间方法。对于 Fisher 法,无论是配对比较还是与对照组进行比较,置信区间的端点和 p 值都是相同的。Fisher 法使用单个置信水平。置信区间公式如下所示:
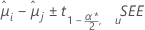
检验统计量的公式为:

p 值 = 2*P{ T u > tu}
要从个别误差率中查找整体置信水平,请使用以下公式:
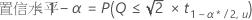
表示法
| 项 | 说明 |
|---|---|
 | 第 i 个因子水平或因子水平组合的最小二乘平均值 |
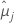 | 第 j 个因子水平或因子水平组合的最小二乘平均值 |
| t1-α*/2, u | 自由度为 u 的学生 t 分布的上侧 α*/2 个百分位数 |
| Tu | 误差自由度为 u 的 T 分布的随机变量 |
| Q | 具有学生化极差分布的随机分量 |
| α | 产生类型 I 错误的整体概率 |
| α* | 产生类型 I 错误的单个概率 |
| u | 模型的误差的自由度 |
| SEE | 最小二乘平均值之间估计差值的标准误 |
Bonferroni 法
公式
Minitab 为比较处理均值提供了不同的置信区间方法。由于 Bonferroni 法未就比较之间的依赖关系做出任何假设,因此它是最保守的方法。该上下文中的“保守”指示实际置信水平有可能大于所显示的置信水平。置信区间公式如下所示:
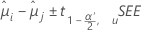
检验统计量的公式为:

表示法
| 项 | 说明 |
|---|---|
 | 第 i 个因子水平或因子水平组合的最小二乘平均值 |
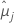 | 第 j 个因子水平或因子水平组合的最小二乘平均值 |
| t1-α*/2, u | 自由度为 u 的学生 t 分布的上侧 α' /2 个百分位数 |
| α | 产生类型 I 错误的整体概率 |
| α' | α / c |
| c | 比较数 |
| u | 模型的误差的自由度 |
| SEE | 最小二乘平均值之间估计差值的标准误 |
比较数量取决于是进行配对比较还是与对照组进行比较。设 k 为要比较的均值的个数。比较数量列在下表中。
| 配对比较 | k (k – 1) / 2 |
| 与对照项进行比较 | k – 1 |
Sidak 法
公式
Minitab 为比较处理均值提供了不同的置信区间方法。Sidak 法将比较视作独立的比较进行处理,这会产生实际误差率的保守近似值。Sidak 方法的功效略高于 Bonferroni 方法。
置信区间公式如下所示:
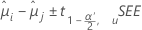
检验统计量的公式为:

调整的 p 值 = 1 − (1 − p)c.
表示法
| 项 | 说明 |
|---|---|
 | 第 i 个因子水平或因子水平组合的最小二乘平均值 |
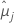 | 第 j 个因子水平或因子水平组合的最小二乘平均值 |
| t1-α*/2, u | 自由度为 u 的学生 t 分布的上侧 α' /2 个百分位数 |
| α | 产生类型 I 错误的整体概率 |
| α' | 1 – (1 – α ) 1/ k |
| u | 模型的误差的自由度 |
| SEE | 最小二乘平均值之间估计差值的标准误 |
| p | 某个比较的 t 分布的未调整的 p 值 |
| c | 比较数 |
比较数量取决于是进行配对比较还是与对照组进行比较。设 k 为因子组合数。比较数量列在下表中。
| 配对比较 | k (k – 1) / 2 |
| 与对照项进行比较 | k – 1 |
Dunnett 法
公式
Minitab 提供了用于比较处理均值的不同置信区间方法。Dunnet 法适用于与对照组进行的比较。置信区间公式如下所示:

检验统计量的公式为:

调整的 p 值是 Dunnett 为检验统计量建议的分布的整合结果。有关详细信息,请查看下面的参考资料。
表示法
| 项 | 说明 |
|---|---|
 | 第 i 个因子水平或因子水平组合的最小二乘平均值 |
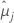 | 第 j 个因子水平或因子水平组合的最小二乘平均值 |
| D1-α, k-1, u | 具有 k − 1 个比较和 u 个自由度的 Dunnett 建议值的分布的上侧 α 百分位数 |
| α | 产生类型 I 错误的整体概率 |
| k | 要比较的均值个数 |
| u | 模型的误差的自由度 |
| SEE | 最小二乘平均值之间估计差值的标准误 |
参考资料
1 Dunnett, C. W.(1955 年 1 月 1 日),A multiple comparison procedure for comparing several treatments with a control(将多个处理与对照组进行比较的多重比较过程),Journal of the American Statistical Association(美国统计协会杂志),第 50 期,第 1096 至 1121 页。
2 J.C. Hsu (1996),Multiple Comparisons: Theory and methods(多重比较:理论和方法),Chapman & Hall。
