N
样本数量 (N) 是每个组中的观测值总数。
解释
样本数量影响置信区间和检验功效。
通常,数量较大的样本将产生较窄的置信区间。样本数量越大,检验检测到差分的功效越大。
均值
每个组中的观测值均值。均值使用确定数据中心的单个值来描述每个组。只需用组的所有观测值的和除以组中的观测值个数即可得出该值。
解释
每个样本的均值提供了每个总体均值的估计值。样本均值之间的差分是总体均值之间差分的估计值。
由于组均值之间的差分均基于样本数据而不是整个总体,因此您不能确定它是否等于总体差分。为更好地了解总体差分,可以使用置信区间。
分组
使用分组信息表快速确定任何组对之间的均值差分是否统计意义显著。
分组列包含对因子水平进行分组的字母。不共享字母的组具有统计意义显著的均值差分。
如果表确定这些差分在统计意义上显著,将使用差分的置信区间来确定差分在实际意义上是否显著。
您可以为随机项执行多重比较分析,以确定哪些项水平与其他水平显著不同。例如,如果您研究某种药物对特定疾病的有效性,受试者通常是显著的随机因子。您可以使用多重比较来确定该药物在研究中是否会对特定受试者产生不同的影响(可能会使其中一个受试者病情加重)。
解释
使用 Tukey 方法和 95% 置信度对信息进行分组
| 油漆 | N | 均值 | 分组 | |
|---|---|---|---|---|
| 配方 4 | 6 | 18.07 | A | |
| 配方 1 | 6 | 14.73 | A | B |
| 配方 3 | 6 | 12.98 | A | B |
| 配方 2 | 6 | 8.57 | B | |
在这些结果中,表显示组 A 包含混料 1、3 和 4,组 B 包含混料 1、2 和 3。混料 1 和混料 3 处于两个组中。共享一个字母的均值之间的差分在统计意义上不显著。混料 2 和混料 4 不共享一个字母,这表明混料 4 的均值比混料 2 的均值明显高很多。
针对均值差分的 Fisher 单独检验
使用单个置信区间来确定组均值之间的差分是否统计意义显著,以确定差分的可能范围,并确定差分是否实际意义显著。Fisher 的单独检验表显示均值对之间差分的一组置信区。
在反复执行研究的情况下,单个置信水平是单个置信区间包含一对组均值间实际差分的次数的百分比。单个置信区间仅对 Fisher 法可用。所有其他比较方法生成整体置信区间。
控制单个置信水平并不通用,因为它无法控制整体置信水平,这通常会提高不可接受的水平。如果您没有控制同步置信水平,则至少有一个置信区间不包含实际差分的概率会随着比较次数的增加而提高。
差分的置信区间由以下两部分组成:
- 点估计
- 点估计是一对均值之间的差分,通过样本数据计算得出。置信区间集中在此值附近。
- 边际误差
- 边际误差定义了置信区间的宽度并由样本和置信水平中的观测变异性确定。要计算置信区间的上限,需要将边际误差与点估计相加。要计算置信区间的下限,需要从点估计减去边际误差。
解释
使用置信区间可评估组均值之间的差分。
均值差值的 Fisher 单个检验
| 水平的差值 | 均值差值 | 差值标准误 | 95% 置信区间 | T 值 | 调整的 P 值 |
|---|---|---|---|---|---|
| 配方 2 - 配方 1 | -6.17 | 2.28 | (-10.92, -1.41) | -2.70 | 0.014 |
| 配方 3 - 配方 1 | -1.75 | 2.28 | (-6.51, 3.01) | -0.77 | 0.452 |
| 配方 4 - 配方 1 | 3.33 | 2.28 | (-1.42, 8.09) | 1.46 | 0.159 |
| 配方 3 - 配方 2 | 4.42 | 2.28 | (-0.34, 9.17) | 1.94 | 0.067 |
| 配方 4 - 配方 2 | 9.50 | 2.28 | (4.74, 14.26) | 4.17 | 0.000 |
| 配方 4 - 配方 3 | 5.08 | 2.28 | (0.33, 9.84) | 2.23 | 0.037 |
- 混料 4 和混料 2 的均值之间差分的置信区间为 (4.74, 14.26)。此范围不包含零,表明这些均值之间的差分在统计意义上显著。
- 混料 2 和混料 1 的均值之间差分的置信区间为 (-10.92, -1.41)。此范围不包含零,表明这些均值之间的差分在统计意义上显著。
- 混料 4 和混料 3 的均值之间差分的置信区间为 (.33, 9.84)。此范围不包含零,表明这些均值之间的差分在统计意义上显著。
- 所有其余均值对的置信区间都包含零,表明这些差分统计意义并不显著。
- 95% 的单个置信水平表明每个置信区间包含特定比较的实际差分的置信度可能为 95%。但是,整体置信水平表明所有区间包含实际差分的置信度可能只有 80.83%。
均值差分
此值是两个组的样本均值之间的差分。
解释
组的样本均值之间的差分是这些组的总体之间的差分估计值。
由于每个均值差分均基于样本数据而不是整个总体,因此您不能确定它是否等于总体差分。为更好地理解总体均值之间的差分,请使用置信区间。
差分标准误
如果从同一总体中反复提取样本,则均值之间的差分标准误(差分 SE)会估计您将获取的样本均值之间差分的变异性。
解释
使用均值之间的差分标准误可确定样本均值之间差分的精确程度,从而估计总体均值之间的差分。标准误的值越低,表明估计值越精确。
Minitab 使用差分标准误来计算均值之间差分的置信区间,它是可能包含总体差分的值范围。
自由度
自由度 (DF) 是数据中的信息量。Minitab 使用自由度为均值差值计算 t 检验。如果您为混合效应模型执行比较,则 Minitab 只会显示自由度。
整体 95% 置信区间
使用差分的整体置信区间(95% 置信区间)可确定均值差分是否在统计意义上显著,从而确定差分的可能范围以及评估差分的实际显著性。表格会显示均值对之间差分的一组置信区间。不包含零的置信区间表示统计意义显著的均值差分。
在多次反复执行研究的情况下,整体置信水平是一组置信区间包含所有组比较值之间实际差分的次数所占的百分比。
在执行多重比较时,控制整体置信水平尤其重要。如果您没有控制同步置信水平,则至少有一个置信区间不包含实际差分的概率会随着比较次数的增加而提高。
有关更多信息,请转到了解多重比较中的单个置信水平和同时置信水平。
差分的置信区间由以下两部分组成:
- 点估计
- 点估计是一对均值之间的差分,通过样本数据计算得出。置信区间集中在此值附近。
- 边际误差
- 边际误差定义了置信区间的宽度并由样本、样本数量和置信水平中的观测变异性确定。要计算置信区间的上限,需要将边际误差与点估计相加。要计算置信区间的下限,需要从点估计减去边际误差。边际会随着比较数的增加而变宽,以便保持所有区间都包含实际总体差分的整体置信水平。
您可以为随机项执行多重比较分析,以确定哪些项水平与其他水平显著不同。例如,如果您研究某种药物对特定疾病的有效性,受试者通常是显著的随机因子。您可以使用多重比较来确定该药物在研究中是否会对特定受试者产生不同的影响(可能会使其中一个受试者病情加重)。
解释
使用置信区间可评估组均值之间的差分。
均值差值的 Tukey 同时检验
| 学科 水平的差值 | 均值差值 | 差值标准误 | 同时 95% 置信区间 | T 值 | 调整的 P 值 |
|---|---|---|---|---|---|
| 2 - 1 | 0.6567 | 0.0664 | (0.4768, 0.8366) | 9.89 | 0.000 |
| 3 - 1 | 0.9633 | 0.0708 | (0.7715, 1.1551) | 13.60 | 0.000 |
| 4 - 1 | 0.6900 | 0.0750 | (0.4870, 0.8930) | 9.20 | 0.000 |
| 3 - 2 | 0.3067 | 0.0632 | (0.1356, 0.4777) | 4.86 | 0.000 |
| 4 - 2 | 0.0333 | 0.0678 | (-0.1502, 0.2169) | 0.49 | 0.960 |
| 4 - 3 | -0.2733 | 0.0721 | (-0.4686, -0.0781) | -3.79 | 0.003 |
- 对象 4 和 2 的均值之间差分的置信区间为 -0.1502 到 0.2169。此范围包含零,表明这些差分在统计意义上不显著。
- 其余均值对的置信区间都不包括零,表明这些差分在统计意义上显著。
- 95% 的整体置信水平表明所有置信区间包含实际差分的置信度可能是 95%。
- 该表指示单个置信水平为 98.94%。此结果表明每个单个区间包含特定组均值对之间实际差分的置信度可能为 98.94%。
- 每个比较的 98.94% 单个置信水平在一起会针对所有六种比较产生 95% 的整体置信水平。
T 值
T 值是一个检验统计量,用来测量均值差值与差值标准误之间的比值。
解释
您可以使用 t 值来确定是否要否定原假设,这表明均值差分为 0。但是,大多数人使用 p 值,因为它更易于解释。有关使用临界值的更多信息,请转到使用 t 值来确定是否要否定原假设。
Minitab 使用 t 值计算 p 值。
调整的 p 值
调整的 p 值表明全族比较中的哪些对显著不同。调整会将全族误差率限制为您指定的 alpha 水平。如果为多重比较使用常规 p 值,则全族误差率会随每个附加比较而增加。
进行多重比较时考虑全族误差率很重要,因为对于一系列比较而言,发生类型 I 错误的几率比单独进行任何一个比较的误差率都要高。
解释
如果调整的 p 值小于 alpha,则否定原假设并得出一对组均值的差值在统计意义上显著。调整的 p 值还表示拒绝特定原假设时的最小全族误差率。
均值差分的区间图
使用置信区间可确定差分的可能范围并评估差分的实际显著性。图形会显示均值对之间差分的一组置信区间。不包含零的置信区间表示统计意义显著的均值差分。
根据您选择的比较方法,图会比较不同的组对并显示下列置信区间类型之一。
-
单个置信水平
在多次反复执行研究的情况下,单个置信区间将包含一对组均值间实际差分的次数的百分比。
-
整体置信水平
在多次反复执行研究的情况下,一组置信区间将包含所有组比较实际差分的次数的百分比。
在执行多重比较时,控制整体置信水平尤其重要。如果您没有控制同步置信水平,则至少有一个置信区间不包含实际差分的概率会随着比较次数的增加而提高。
有关更多信息,请转到了解多重比较中的单个置信水平和同时置信水平。
您可以为随机项执行多重比较分析,以确定哪些项水平与其他水平显著不同。例如,如果您研究某种药物对特定疾病的有效性,受试者通常是显著的随机因子。您可以使用多重比较来确定该药物在研究中是否会对特定受试者产生不同的影响(可能会使其中一个受试者病情加重)。
解释
使用置信区间可评估组均值之间的差分。
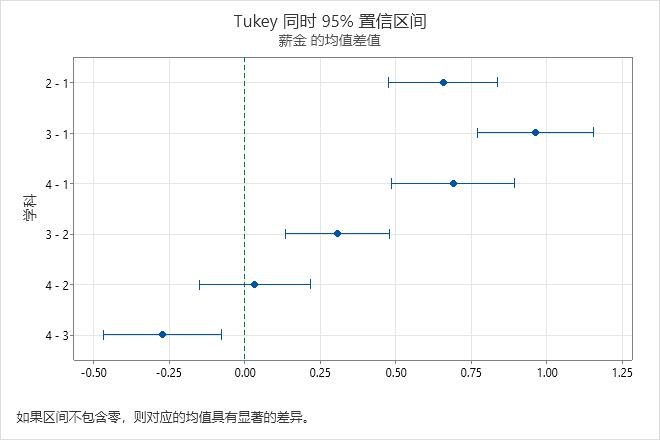
均值差值的 Tukey 同时检验
| 学科 水平的差值 | 均值差值 | 差值标准误 | 同时 95% 置信区间 | T 值 | 调整的 P 值 |
|---|---|---|---|---|---|
| 2 - 1 | 0.6567 | 0.0664 | (0.4768, 0.8366) | 9.89 | 0.000 |
| 3 - 1 | 0.9633 | 0.0708 | (0.7715, 1.1551) | 13.60 | 0.000 |
| 4 - 1 | 0.6900 | 0.0750 | (0.4870, 0.8930) | 9.20 | 0.000 |
| 3 - 2 | 0.3067 | 0.0632 | (0.1356, 0.4777) | 4.86 | 0.000 |
| 4 - 2 | 0.0333 | 0.0678 | (-0.1502, 0.2169) | 0.49 | 0.960 |
| 4 - 3 | -0.2733 | 0.0721 | (-0.4686, -0.0781) | -3.79 | 0.003 |
- 受试对象 4 和受试对象 2 的均值差值的置信区间为 -0.1502 至 0.2169。此范围包括零,表明差值在统计意义上不显著。
- 其余均值对的置信区间都不包括零,表明这些差值在统计意义上显著。
- 95% 的整体置信水平表明所有置信区间包含实际差分的置信度可能是 95%。
- 该表指示单个置信水平为 98.94%。此结果表明每单个区间包含特定组均值对之间实际差值的置信度为 98.94%。
- 每个比较的 98.94% 单个置信水平在一起会针对所有六种比较产生 95% 的整体置信水平。
