双指数平滑在每个周期处采用水平分量和趋势分量。它使用两个权重(即平滑参数)在每个周期处更新分量。双指数平滑方程为:
- Lt = α Yt + (1 - α) [Lt-1 + Tt-1]
- Tt = γ[Lt - Lt-1] + (1 - γ) Tt-1
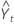 = Lt-1 + Tt-1
= Lt-1 + Tt-1
其中 Lt 是时间 t 处的水平,α 是水平的权重,Tt 是时间 t 处的趋势,γ 是趋势的权重,Yt 是时间 t 处的数据值,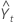 是时间 t 处的拟合值(即向前一步的预测)。
是时间 t 处的拟合值(即向前一步的预测)。
第一个观测值编号为一,因此,必须将时间零处的水平和趋势估计值初始化才能继续。初始化方法用于确定如何以两种方式之一获取平滑值:使用 Minitab 生成的权重或者使用指定的权重。
| 最优 ARIMA 权重 | 指定的权重 |
|---|---|
|
|
指定对应于等根 ARIMA (0, 2, 2) 模型的权重时,Holt 方法特殊化为 Brown 方法。
