Minitab® 支持

Winter 方法 的方法和公式

了解关于 Minitab 的更多信息
请选择您所选的方法或公式。

关于本主题

乘法

公式

乘法模型为：

  • Lt = α (Yt / St–p) + (1 – α) [Lt–1 + Tt–1]
  • Tt = γ [Lt – Lt–1] + (1 – γ) Tt–1
  • St = δ (Yt / Lt) + (1 – δ) St–p
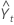  • = (Lt–1 + Tt–1) St–p

表示法

项说明
Lt在时间 t 的水平，α 是水平的权重
Tt在时间 t 的趋势，
γ趋势的权重
St在时间 t 的季节性分量
δ季节性分量的权重
p季节性周期
Yt在时间 t 的数据值
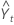在时间 t 的拟合值（或提前一个周期预测）

乘法模型水平和趋势初始值的计算方法

以下方法假定季节长度大于 4。

  1. 查找数据的平均值、最小值和最大值。例如：
    • 平均值 = 554.208
    • 最小值 = 1
    • 最大值 = 1498.47
  2. 对于每行数据，计算：
  3. 设 N 等于季节长度。对于此例，N = 12。
  4. 使用第一个 N“临时值”（在步骤 2 中计算）作为 Y 变量并使用 1 到 N 的向量作为 X 变量来运行回归。因此，对于本示例：
    Y X
    4104.36 1
    4104.36 2
    4630.36 3
    4922.80 4
    4822.40 5
    5601.83 6
    4891.77 7
    4604.44 8
    4411.26 9
    4123.66 10
    4104.36 11
    4104.36 12

    回归线的斜率是趋势的初始值。

  5. 通过相减来调整回归线的截距：

数据的截距为 4705.24。从截距中减去 4103.36，获得调整后的截距 601.879。此调整的截距是水平的初始值。

加法

公式

加法模型为：
  • Lt = α (Yt – St–p) + (1 – α) [Lt–1 + Tt–1]
  • Tt = γ [Lt – Lt–1] + (1 – γ) Tt–1
  • St = δ (Yt – Lt) + (1 – δ) St–p
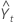  • = Lt–1 + Tt–1 + St–p

表示法

项说明
Lt在时间 t 的水平，α 是水平的权重
Tt在时间 t 的趋势，
γ趋势的权重
St在时间 t 的季节性分量
δ季节性分量的权重
p季节性周期
Yt在时间 t 的数据值
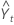在时间 t 的拟合值（或提前一个周期预测）

加法模型水平和趋势初始值的计算方法

以下方法假定季节长度大于 4。

  1. 设 N 等于季节长度。对于此例，N = 12。
  2. 使用前 N 个数据值作为 Y 变量并使用 1 到 N 的向量作为 X 变量来运行回归。因此，对于本示例：
    Y X
    1.00 1
    1.00 2
    527.00 3
    819.45 4
    719.04 5
    1498.47 6
    788.42 7
    501.08 8
    307.90 9
    20.30 10
    1.00 11
    1.00 12

    回归线的斜率是趋势的初始值。回归线的截距是水平的初始值。

加法模型的季节性指数的初始值计算方法

以下方法假定季节长度大于 4。

  1. 使用数据值作为 Y 变量并使用 1 到 24 的向量作为 X 变量来运行回归。因此，对于本示例：
    Y X
    1.00 1
    1.00 2
    527.00 3
    819.45 4
    719.04 5
    1498.47 6
    788.42 7
    501.08 8
    307.90 9
    20.30 10
    1.00 11
    1.00 12
    83.00 13
    668.21 14
    1121.28 15
    1386.84 16
    1031.18 17
    988.60 18
    1380.30 19
    1005.97 20
    233.69 21
    211.87 22
    2.00 23
    2.40 24

    在下一步使用此回归模型的残差

  2. 使用残差作为 Y 变量并使用 12 个指示变量（z.1 到 z.12）作为 X 变量来运行回归。拟合没有截距（常量）项的回归模型。因此，对于本示例：
    残差 z.1 z.2 z.3 z.4 z.5 z.6 z.7 z.8 z.9 z.10 z.11 z.12
    -508.261 1 0 0 0 0 0 0 0 0 0 0 0
    -512.170 0 1 0 0 0 0 0 0 0 0 0 0
    9.926 0 0 1 0 0 0 0 0 0 0 0 0
    298.460 0 0 0 1 0 0 0 0 0 0 0 0
    194.145 0 0 0 0 1 0 0 0 0 0 0 0
    969.667 0 0 0 0 0 1 0 0 0 0 0 0
    255.705 0 0 0 0 0 0 1 0 0 0 0 0
    -35.538 0 0 0 0 0 0 0 1 0 0 0 0
    -232.625 0 0 0 0 0 0 0 0 1 0 0 0
    -524.137 0 0 0 0 0 0 0 0 0 1 0 0
    -547.346 0 0 0 0 0 0 0 0 0 0 1 0
    -551.254 0 0 0 0 0 0 0 0 0 0 0 1
    -473.161 1 0 0 0 0 0 0 0 0 0 0 0
    108.141 0 1 0 0 0 0 0 0 0 0 0 0
    557.303 0 0 1 0 0 0 0 0 0 0 0 0
    818.952 0 0 0 1 0 0 0 0 0 0 0 0
    459.378 0 0 0 0 1 0 0 0 0 0 0 0
    412.890 0 0 0 0 0 1 0 0 0 0 0 0
    800.684 0 0 0 0 0 0 1 0 0 0 0 0
    422.451 0 0 0 0 0 0 0 1 0 0 0 0
    -353.739 0 0 0 0 0 0 0 0 1 0 0 0
    -379.468 0 0 0 0 0 0 0 0 0 1 0 0
    -593.247 0 0 0 0 0 0 0 0 0 0 1 0
    此回归模型的系数是季节性指数的初始值。系数为：
    阶段 COEF1
    1 -490.711
    2 -202.014
    3 283.615
    4 558.706
    5 326.762
    6 691.278
    7 528.195
    8 193.456
    9 -293.182
    10 -451.803
    11 -570.297
    12 -574.005
    注意

    指示变量 z.1 到 z.12 表示每个数据点所属的周期的哪个月。例如，变量 z.1 在该周期第一个月等于 1，否则等于 0。

模型拟合

Winters 方法在每个周期中采用一个水平分量、一个趋势分量以及一个季节性分量。它在每个周期使用三个权重（即平滑参数）来更新分量。水平和趋势分量的初始值从对时间进行线性回归而来。季节性分量的初始值则从使用去除趋势后的数据的虚拟变量回归而来。

预测

Winters 方法使用水平、趋势和季节性分量来生成预测。Winters 方法还使用预测起始时间之前的数据来生成预测。

公式

对时间点 t 向前 m 个周期的预测为：
  • 乘法方法：(Lt + mTt) * St + m −p
  • 加法方法：Lt + mTt +St + m −p

表示法

项说明
Lt水平
Tt时间 t 处的趋势
项说明
St + m −p上一年中同一周期的季节性分量

平均绝对百分比误差 (MAPE)

平均绝对百分比误差 (MAPE) 度量时间序列值拟合的准确度。MAPE 以百分比表示准确度。

公式

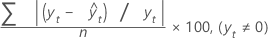
表示法

项说明
yt 时间 t 处的实际值
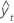拟合值
n 观测值个数

平均绝对误差 (MAD)

平均绝对偏差 (MAD) 度量时间序列值拟合的准确度。MAD 以与数据相同的单位表示准确度，从而有助于使误差量概念化。

公式

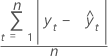
表示法

项说明
yt 时间 t 处的实际值
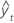拟合值
n 观测值个数

平均偏差平方和 (MSD)

无论采用哪种模型，平均偏差平方和 (MSD) 始终是使用相同的分母 n 计算的。对于异常大的预测误差，MSD 度量比 MAD 敏感。

公式

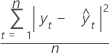
表示法

项说明
yt 时间 t 处的实际值
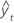拟合值
n 观测值个数
Copyright © 2024 Minitab, LLC. All rights Reserved.