关于本主题
长度
时间序列中观测值的数量。
α(水平)
α 是平滑估计值的水平分量中使用的权重。α 类似于观测值的移动平均值。权重通过定义每个分量对当前条件的响应方式来调整平滑量。权重越低,赋予最近数据的权重越低。权重越高,赋予最近数据的权重越高。调整水平分量的权重通常能够获得改善准确度度量的最佳机会。在将水平权重调整到所需的大小之后,更改其他权重所产生的效应通常较小。
γ(趋势)
权重越高,对最近数据的影响越大,因此预测值(绿色)服从数据(黑色)末端的向下趋势。
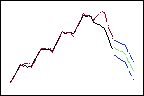
较高的趋势权重
权重越低,对最近数据的影响越大,因此预测值服从整体的向上趋势。
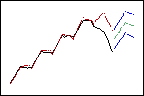
较小的趋势权重
δ(季节性)
δ 是平滑估计值的季节性分量中使用的权重。权重通过定义每个分量对当前条件的响应方式来调整平滑量。权重越低,赋予最近数据的权重越低。权重越高,赋予最近数据的权重越高。
平均绝对百分比误差 (MAPE)
平均绝对百分比误差 (MAPE) 以误差的百分比来表示准确度。由于 MAPE 是一个百分比值,因此它可能比其他准确度度量统计量更容易理解。例如,如果 MAPE 为 5,则表示预测平均偏离 5%。
但是,有时,您可能会发现非常大的 MAPE 值,即使模型看上去能够很好地拟合数据也是如此。检查该图以查看任何数据值是否接近 0。由于 MAPE 将绝对误差除以实际数据,因此接近 0 的值可能会使 MAPE 显著增加。
解释
用来比较不同时间序列模型的拟合度。值越小表示拟合得越好。如果单个模型对于所有 3 个准确度度量没有最低值,则 MAPE 通常是首选度量。
准确度度量基于提前一个周期的残差。在每个时间点,模型用于为下一个时间段预测 Y 值。预测值(拟合值)和实际 Y 之间的差异是提前一个周期的残差。因此,准确度度量提供在您预测数据末端外 1 个周期的值时可能遇到的准确度表示。所以,准确度度量不指示 1 个周期以外的预测准确度。如果您要使用模型进行预测,则不应当仅基于准确度度量做出决策。您还应当检查模型的拟合度以确保预测值和模型沿着数据紧密分布,尤其是在序列末端。
平均绝对误差 (MAD)
平均绝对偏差 (MAD) 以与数据相同的单位表示准确度,从而有助于使误差量概念化。异常值对 MAD 的影响比对 MSD 的影响小。
解释
用来比较不同时间序列模型的拟合度。值越小表示拟合得越好。
准确度度量基于提前一个周期的残差。在每个时间点,模型用于为下一个时间段预测 Y 值。预测值(拟合值)和实际 Y 之间的差异是提前一个周期的残差。因此,准确度度量提供在您预测数据末端外 1 个周期的值时可能遇到的准确度表示。所以,准确度度量不指示 1 个周期以外的预测准确度。如果您要使用模型进行预测,则不应当仅基于准确度度量做出决策。您还应当检查模型的拟合度以确保预测值和模型沿着数据紧密分布,尤其是在序列末端。
平均偏差平方和 (MSD)
平均偏差平方和 (MSD) 度量时间序列值拟合的准确度。异常值对 MSD 的影响比对 MAD 的影响大。
解释
用来比较不同时间序列模型的拟合度。值越小表示拟合得越好。
准确度度量基于提前一个周期的残差。在每个时间点,模型用于为下一个时间段预测 Y 值。预测值(拟合值)和实际 Y 之间的差异是提前一个周期的残差。因此,准确度度量提供在您预测数据末端外 1 个周期的值时可能遇到的准确度表示。所以,准确度度量不指示 1 个周期以外的预测准确度。如果您要使用模型进行预测,则不应当仅基于准确度度量做出决策。您还应当检查模型的拟合度以确保预测值和模型沿着数据紧密分布,尤其是在序列末端。
平滑
平滑数据是水平分量与季节性分量的总和(加法模型),或者水平分量与季节性分量的乘积(乘法模型)。
预测
预测值又称为拟合值。预测值是时间 (t) 处变量的点估计值。
其预测值与观测值显著不同的观测值可能是异常值或有影响的值。尝试确定导致任何异常值的原因。更正任何数据输入错误或测量误差。考虑删除与异常的单次事件(也称为特殊原因)相关联的数据值。然后,重新执行分析。
误差
误差值又称为残差。误差值是观测值和预测值之间的差异。
解释
绘制误差值图可以确定模型是否充分。误差值可以提供有关模型对数据的拟合优度的有用信息。通常,误差值应当随机分布在 0 周围,而且没有明显模式和异常值。
周期
当您生成预测值时,Minitab 显示周期。周期是预测值的时间单位。默认情况下,预测值始于数据末端。
预测
预测值是从时间序列模型获取的拟合值。Minitab 显示您指定的预测值个数。预测值始于数据末端或者您指定的原点处。
解释
使用预测可以为指定的时间段预测某个变量。例如,一位仓库经理可以基于前 60 个月的订单预测接下来的 3 个月中需要订购多少产品。
检查图中的拟合及预测值,确定预测值是否有可能准确。拟合应当沿着数据紧密分布,尤其是在序列末端。在使用季节性模型时,验证时间序列末端的拟合值与实际值是否匹配尤其重要。如果数据末端的季节性模式或趋势与拟合值不匹配,则说明预测值可能不够准确。在这种情况下,请收集更多的数据,以便模型可以适应季节性模式或趋势的改变。
如果模型与序列末端的数据相拟合,通常可以安全地预测至少一个完整的季节性周期。
下限和上限
预测下限和上限会为每个预测值生成一个预测区间。预测区间是预测的一系列可能值。例如,使用 95% 预测区间,可以 95% 地确信预测区间包含指定时间处的预测值。
Winters 方法图
该图显示观测值与时间的关系。该图包括根据平滑过程计算的拟合值、预测值、平滑常量和准确度度量。您还可以选择显示平滑值(而非拟合值)。
解释
- 如果模型与数据拟合,则可以执行 分解 并比较两个模型。
- 如果模型与数据不拟合,请检查图中是否缺乏季节性模式。如果没有季节性模式,则应当使用其他时间序列分析。有关更多信息,请转到应当使用哪些时间序列分析?。
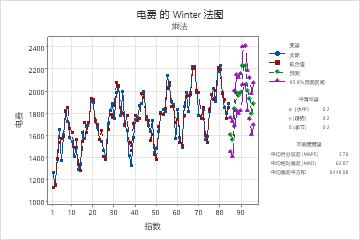
在该图中,拟合值沿着数据紧密分布,这表明模型与数据拟合。
残差的直方图
残差的直方图显示所有观测值的残差的分布情况。如果模型与数据很好地拟合,则残差应当随机分布且均值为 0。因此,直方图应当相对于 0 大致对称。
残差的正态概率图
残差的正态图显示当分布服从正态时残差与期望值的关系。
解释
使用残差的正态图可以确定残差是否呈正态分布。但是,此分析不要求残差呈正态分布。
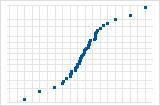
S 曲线表示长尾分布。
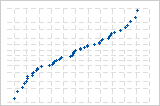
反向 S 曲线表示短尾分布。
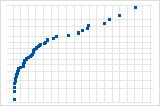
向下的曲线表示右偏斜分布。
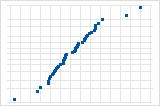
远离线的几个点表示分布中有异常值。
残差与拟合值
残差与拟合图在 y 轴上显示残差,在 x 轴上显示拟合值。
解释
使用残差与拟合值的关系图可以确定残差是否不偏斜且具有恒定的方差。理想情况是,点应当随机落在两端(0 处),点中没有可识别的模式。
| 模式 | 模式的含义 |
|---|---|
| 残差相对拟合值呈扇形或不均匀分散 | 异方差 |
| 曲线 | 缺少高次项 |
| 远离 0 的点 | 异常值 |
如果您在残差中看到非恒定的方差或模式,则说明预测值可能不准确。
残差与顺序
残差与顺序的关系图按照数据的收集顺序显示残差。
解释
使用残差与顺序的关系图可以确定在观测期间内,拟合值相对于观测值的准确度。点中的模式可能指示模型与数据不拟合。理想情况是,图上的残差应围绕中心线随机分布。
| Pattern | 模式的含义 |
|---|---|
| 一致的长期趋势 | 模型与数据不拟合 |
| 短期趋势 | 模式中的偏移或变化 |
| 远离其他点的点 | 异常值 |
| 点中的突然偏移 | 数据的基础模式已改变 |
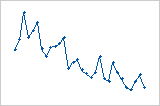
随着观测值的顺序从左到右提高,残差以系统方式降低。
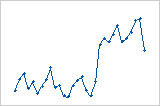
残差的值从低(左)到高(右)突然变化。
残差与变量
残差与变量的关系图显示残差与另一个变量的关系。
解释
使用该图可以确定变量是否会以系统方式对响应造成影响。如果残差中存在模式,则说明其他变量与响应相关联。您可以使用此信息作为其他研究的基础。
