偏自相关函数用来度量暂时调整所有其他较短滞后的项 (yt–1, yt–2, ..., yt–k–1) 之后,时间序列中以 k 个时间单位(yt 和 yt–k)分隔的观测值之间的相关。
解释
结合使用自相关函数和偏自相关函数来确定 ARIMA 模型。在偏自相关函数上查找下面的模式。检查每个滞后处的峰值以确定它们是否显著。显著的峰值将超出显著限,这表明该滞后的相关不等于零。
| 模式 | 表明 | 示例 |
|---|---|---|
| 滞后 1 处的峰值,在几个滞后以后减小。 | 数据中的移动平均项。使用自相关函数可以确定移动平均项的阶次。 | 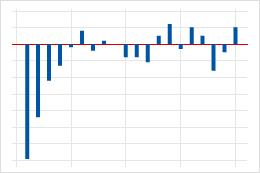 |
| 滞后 1 处的峰值较大,后面是一个在正相关和负相关之间交替的阻尼波。 | 数据中的高阶移动平均项。使用自相关函数可以确定移动平均项的阶次。 | 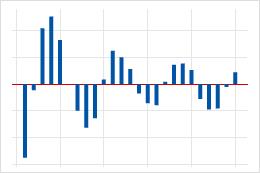 |
| 第一个或第二个滞后处的显著相关,后面是不显著的相关。 | 数据中的自回归项。显著相关的个数指示自回归项的阶次。 | 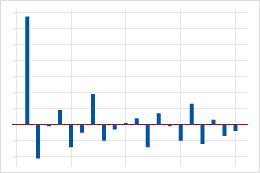 |
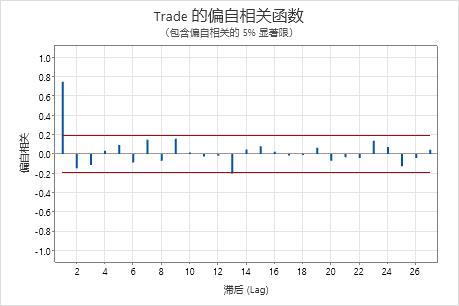
在该图中,滞后 1 处有一个显著相关,后面是不显著的相关。此模式指示 1 阶自回归项。
