移动平均
要计算移动平均值,Minitab 求一个序列中多组连续观测值的平均值。例如,假设一个序列始于“4、5、8、9、10”,而且您使用的移动平均长度为 3。前两个移动平均值是缺失的。第三个移动平均值是 4、5 和 8 的平均值,第四个值是 5、8 和 9 的平均值,第五个值是 8、9 和 10 的平均值。
居中的移动平均
默认情况下,移动平均值位于用于计算它们的周期处。例如,对于长度为 3 的移动平均,第一个数字移动平均值位于周期 3 处,第二个位于周期 4 处,依此类推。
使移动平均居中时,将其置于范围的中心而不是末尾。这样做可将移动平均值置于其时间中心位置。
如果移动平均长度为奇数
假定移动平均长度为 3。在这种情况下,Minitab 将第一个数字移动平均值放在周期 2 处,将第二个移动平均值放在周期 3 处,依此类推。在这种情况下,第一个和最后一个周期的移动平均值为缺失 (*)。
如果移动平均长度为偶数
假定移动平均长度为 4。由于您无法将移动平均值放在周期 2.5 处,因此 Minitab 计算前四个值的平均值并将其命名为 MA1。然后 Minitab 计算接下来四个值的平均值并将其命名为 MA2。Minitab 将这两个值的平均值放在周期 3 处。在这种情况下,前两个周期和最后两个周期的移动平均值为缺失 (*)。
预测
时间 t 处的拟合值是时间 t – 1 处的非居中移动平均值。预测值是预测原点处的拟合值。如果提前 10 个时间单位预测,则每个时间的预测值将是原点处的拟合值。原点之前的数据用于计算移动平均。
通过执行连续移动平均,可以使用线性移动平均法。当数据中存在趋势时,通常这样做。首先,计算并存储原始序列的移动平均。然后,计算并存储先前存储的列的移动平均以得到第二个移动平均。
在单纯预测中,时间 t 的预测是时间 t – 1 处的数据值。对长度为一的移动平均使用移动平均过程会得到单纯预测。
预测限
公式
上限 = 预测值 + 1.96 × 
下限 = 预测值 – 1.96 × 
表示法
| 项 | 说明 |
|---|---|
| MSD | 均方差 |
平均绝对百分比误差 (MAPE)
平均绝对百分比误差 (MAPE) 度量时间序列值拟合的准确度。MAPE 以百分比表示准确度。
公式
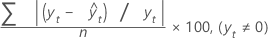
表示法
| 项 | 说明 |
|---|---|
| yt | 时间 t 处的实际值 |
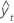 | 拟合值 |
| n | 观测值个数 |
平均绝对误差 (MAD)
平均绝对偏差 (MAD) 度量时间序列值拟合的准确度。MAD 以与数据相同的单位表示准确度,从而有助于使误差量概念化。
公式
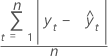
表示法
| 项 | 说明 |
|---|---|
| yt | 时间 t 处的实际值 |
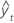 | 拟合值 |
| n | 观测值个数 |
平均偏差平方和 (MSD)
无论采用哪种模型,平均偏差平方和 (MSD) 始终是使用相同的分母 n 计算的。对于异常大的预测误差,MSD 度量比 MAD 敏感。
公式
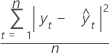
表示法
| 项 | 说明 |
|---|---|
| yt | 时间 t 处的实际值 |
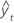 | 拟合值 |
| n | 观测值个数 |
