完成以下步骤以解释模型选择过程和 ARIMA 分析的结果。主要输出包括模型选择统计量、p 值、系数、长盒卡方统计量和残差的自相关函数。
步骤 1:考虑替代模型
“模型选择”表显示搜索中每个模型的条件。该表显示项的顺序,其中 p 是自回归项,d 是差分项,q 是移动平均项。季节性术语使用大写字母,非季节性术语使用小写字母。
使用 AIC、AICc 和 BIC 比较不同的模型。值越小越合意。但是,对于一组项具有最小值的模型不一定能很好地拟合数据。使用测试和绘图来评估模型与数据的拟合程度。默认情况下,ARIMA 结果适用于具有最佳 AICc 值的模型。
选择 选择备择模型 此选项可打开包含“模型选择”表的对话框。比较条件以调查具有相似性能的模型。
使用 ARIMA 输出验证模型中的项是否具有统计显著性,以及模型是否符合分析的假设。如果表中没有一个模型与数据拟合良好,请考虑具有不同差异顺序的模型。
当替代模型的性能几乎与最佳模型一样好,并且自回归项和移动平均数具有较低的阶数时,还要考虑使用替代模型。具有较少项的模型更易于解释,并且可以具有更好的预测能力。具有较少项的模型也不太可能包含冗余项。例如,季节性自回归项有时与季节性移动平均线项是多余的。冗余项有时会使系数的估计值不稳定。以下是不稳定系数导致的一些后果:
- 即使预测变量和响应之间存在显著关系,系数也可能看起来并不显著。
- 高度相关的预测变量的系数在样本之间差异很大。
- 从模型中去除任何高度相关的项都将大幅影响其他高度相关项的估计系数。高度相关项的系数甚至会包含错误的符号。
模型选择
| 模型 (d = 1) | 对数似然 | AICc | AIC | BIC |
|---|---|---|---|---|
| p = 0, q = 2* | -197.052 | 400.878 | 400.103 | 404.769 |
| p = 1, q = 2 | -196.989 | 403.311 | 401.978 | 408.199 |
| p = 1, q = 0 | -201.327 | 407.029 | 406.654 | 409.765 |
| p = 2, q = 0 | -200.239 | 407.251 | 406.477 | 411.143 |
| p = 1, q = 1 | -200.440 | 407.655 | 406.880 | 411.546 |
| p = 2, q = 1 | -201.776 | 412.884 | 411.551 | 417.773 |
| p = 0, q = 1 | -204.584 | 413.542 | 413.167 | 416.278 |
| p = 0, q = 0 | -213.614 | 429.350 | 429.229 | 430.784 |
主要结果AICc、BIC 和 AIC
ARIMA(0, 1, 2) 具有 AICc 的最佳值。下面的 ARIMA 结果适用于 ARIMA(0, 1, 2) 模型。如果模型不能很好地拟合数据,请考虑具有类似性能的其他模型,例如 ARIMA(1, 1, 2) 模型和 ARIMA (1, 1, 1) 模型。如果所有模型都不能很好地拟合数据,请考虑是否使用其他类型的模型。
步骤 2:确定模型中的每个项是否显著
要确定响应与模型中每个项之间的关联在统计意义上是否显著,请将该项的 P 值与显著性水平进行比较以评估原假设。原假设是项与 0
没有显著差异,这表明项和响应之间不存在关联。通常,显著性水平(用 α 或 alpha 表示)为 .05 即可。显著性水平为 0.05 表示当项与 0
显著不同时,得出项与 0 没有显著差异的结论的风险为 5%。
- P-值 ≤ α: 该术语在统计意义上显著
- 如果 p 值小于或等于显著性水平,则可以得出系数在统计意义上显著的结论。
- P-值 > α: 该术语在统计意义上不显著
- 如果 p 值大于显著性水平,则不能得出系数在统计意义上显著的结论。您可能希望重新拟合没有该项的模型。
参数的最终估计值
| 类型 | 系数 | 系数标准误 | T 值 | P 值 |
|---|---|---|---|---|
| AR 1 | -0.504 | 0.114 | -4.42 | 0.000 |
| 常量 | 150.415 | 0.325 | 463.34 | 0.000 |
| 均值 | 100.000 | 0.216 |
关键结果:P, 科夫
自回归项的 p 值小于显著性水平 .0.05。您可以得出自回归项的系数在统计意义上显著的结论,而且您应当将它们保留在模型中。
步骤 3:确定模型是否符合分析的假设
使用残差的 Ljung-Box 卡方统计量和自相关函数可以确定模型是否符合残差保持独立这一假设。如果未满足此假设,则模型可能无法拟合数据,在解释结果时应当格外小心。
- Ljung-Box 卡方统计量
- 要确定残差是否独立,请比较每个卡方统计量的 p 值与显著性水平。通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。如果 p 值大于显著性水平,则可以得出残差独立且模型符合假设的结论。
- 残差的自相关函数
- 如果不存在显著的相关,则可以得出残差独立的结论。但是,在较高阶的非季节性滞后处,您可能会看到 1 个或 2 个显著相关。这些相关通常是由随机误差引起的,它们并不说明未满足假设。在这种情况下,您可以得出残差保持独立的结论。
修正 Box-Pierce(Ljung-Box) 卡方统计量
| 滞后 (Lag) | 12 | 24 | 36 | 48 |
|---|---|---|---|---|
| 卡方 | 4.05 | 12.13 | 25.62 | 32.09 |
| 自由度 | 10 | 22 | 34 | 46 |
| P 值 | 0.945 | 0.955 | 0.849 | 0.940 |
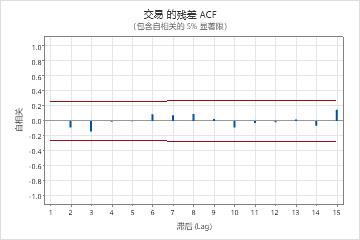
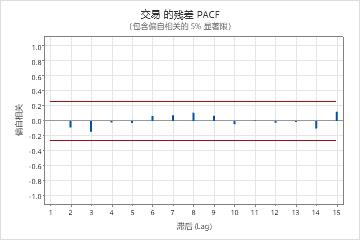
主要结果:P 值,残差的 ACF
在这些结果中,Ljung-Box 卡方统计量的 p 值均大于 0.05,残差的自相关函数的任何相关都不显著。您可以判定模型符合残差保持独立这一假设。
