使用最佳 ARIMA 模型进行预测季节性模型的示例

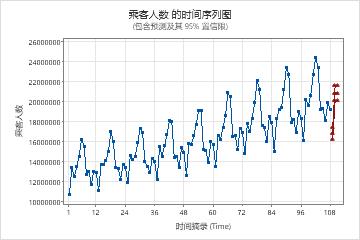
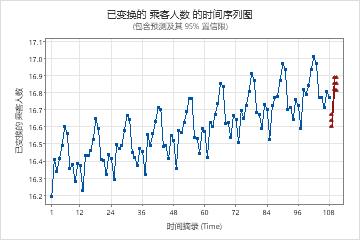
一位分析师收集了108个月的航空公司乘客人数数据。分析师希望使用 ARIMA 模型为数据生成预测。该分析师之前检查了数据的时间序列图，并观察到季节性周期的变化随时间而增加。分析师的结论是，对数据进行自然对数转换是合适的。转换后，分析人员检查了已转换数据的时间序列图和已转换数据的自相关函数（ACF）图。这两个图都表明，模型的起点是选择 1 作为非季节性差分的顺序，选择 1 作为季节性差分的顺序。分析师要求对未来 3 个月进行预测。

打开样本数据航空乘客.mtw。
选择统计 > 时间序列 > 使用最佳 ARIMA 模型进行预测。
在序列中，输入乘客人数。
在中差分阶次 d，选择 1。
选择将季节性模型与周期拟合并输入 12 作为时间段。
在中季节性差分阶次 D，选择 1。
在预测点数中，输入 3。
选择选项。
在Box-Cox 变换中，选择 λ = 0 (自然对数)。
单击每个对话框中的确定。

解释结果

模型选择表按 AICc 的顺序对搜索中的模型进行排名。ARIMA（0， 1， 1）（1， 1， 0）模型具有最少的 AICc。下面的 ARIMA 结果适用于 ARIMA（0， 1， 1）（1， 1， 0）模型。

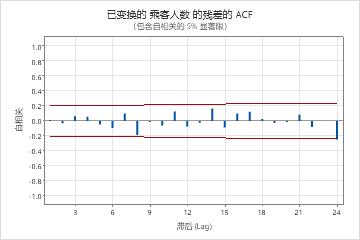
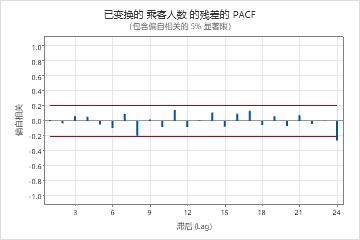
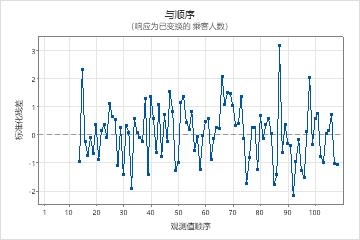
参数表中的 p 值表明模型项在 0.05 水平上是显著的。分析人员得出结论，系数属于模型。修改后的箱形皮尔斯（Ljung-Box）统计量的 p 值在 0.05 水平上都是微不足道的。残差的 ACF 和残差的 PACF 在滞后 24 处显示峰值。由于高滞后数处的大峰值通常是误报，并且检验统计量都无关紧要，因此分析人员得出结论，该模型符合残差独立的假设。分析师的结论是，对预测的检查是合理的。

季节周期	12
最佳模型的标准	最小 AICc
Box-Cox 变换
用户指定的 λ	0
已变换的序列 = ln(乘客人数)
已使用的行数	108
未使用的行	0

模型 (d = 1, D = 1)	对数似然	AICc	AIC	BIC
p = 0, q = 1, P = 1, Q = 0*	243.477	-480.690	-480.954	-473.292
p = 2, q = 0, P = 0, Q = 1	243.903	-479.362	-479.806	-469.590
p = 1, q = 1, P = 1, Q = 0	243.496	-478.547	-478.992	-468.776
p = 0, q = 2, P = 1, Q = 0	243.480	-478.516	-478.961	-468.745
p = 2, q = 0, P = 1, Q = 1	244.424	-478.174	-478.848	-466.079
p = 0, q = 1, P = 0, Q = 0	237.930	-471.729	-471.859	-466.752
p = 1, q = 2, P = 0, Q = 0	239.930	-471.415	-471.859	-461.644
p = 1, q = 1, P = 0, Q = 0	237.929	-469.594	-469.858	-462.196
p = 0, q = 2, P = 0, Q = 0	237.924	-469.584	-469.848	-462.186
p = 1, q = 0, P = 0, Q = 1	237.442	-468.619	-468.883	-461.221
p = 1, q = 0, P = 1, Q = 1	237.551	-466.658	-467.102	-456.887
p = 2, q = 2, P = 0, Q = 0	238.267	-465.860	-466.534	-453.765
p = 2, q = 0, P = 0, Q = 0	232.478	-458.693	-458.957	-451.295
p = 0, q = 0, P = 0, Q = 1	226.062	-447.993	-448.124	-443.016
p = 0, q = 0, P = 1, Q = 1	226.282	-446.300	-446.563	-438.902
p = 2, q = 1, P = 0, Q = 0	226.105	-443.766	-444.211	-433.995
p = 1, q = 0, P = 0, Q = 0	222.409	-440.687	-440.818	-435.710
p = 2, q = 0, P = 1, Q = 0	220.456	-432.467	-432.911	-422.696
p = 0, q = 0, P = 1, Q = 0	218.236	-432.342	-432.472	-427.364
p = 1, q = 2, P = 1, Q = 1	220.708	-428.461	-429.416	-414.092
p = 0, q = 2, P = 0, Q = 1	215.116	-421.787	-422.232	-412.016
p = 0, q = 1, P = 0, Q = 1	213.007	-419.751	-420.015	-412.353
p = 2, q = 1, P = 0, Q = 1	214.469	-418.265	-418.939	-406.169
p = 1, q = 0, P = 1, Q = 0	211.232	-416.199	-416.463	-408.801
p = 2, q = 2, P = 0, Q = 1	213.877	-414.799	-415.754	-400.431
p = 2, q = 2, P = 1, Q = 1	214.698	-414.109	-415.397	-397.520
p = 1, q = 2, P = 0, Q = 1	211.492	-412.310	-412.984	-400.215
p = 1, q = 1, P = 0, Q = 1	208.149	-407.854	-408.299	-398.083
p = 0, q = 1, P = 1, Q = 1	204.745	-401.046	-401.490	-391.275
p = 0, q = 2, P = 1, Q = 1	203.978	-397.282	-397.956	-385.187
p = 1, q = 1, P = 1, Q = 1	203.564	-396.453	-397.127	-384.358
p = 1, q = 2, P = 1, Q = 0	170.812	-330.950	-331.624	-318.855
p = 2, q = 2, P = 1, Q = 0	167.845	-322.735	-323.690	-308.367
p = 2, q = 1, P = 1, Q = 0	-202.538	415.751	415.076	427.846

类型	系数	系数标准误	T 值	P 值
SAR 12	-0.403	0.103	-3.92	0.000
MA 1	0.8704	0.0510	17.08	0.000

滞后 (Lag)	12	24	36	48
卡方	9.47	26.44	33.99	50.66
自由度	10	22	34	46
P 值	0.489	0.233	0.468	0.295

		95% 限值
时间周期	预测	下限	上限	实际
109	16822664	16227242	17434097
110	20823876	20080751	21587153
111	20826702	20077443	21596450

使用最佳 ARIMA 模型进行预测季节性模型的示例

解释结果

方法

模型选择

参数的最终估计值

模型汇总

修正 Box-Pierce(Ljung-Box) 卡方统计量

原始序列

已变换的序列

			95% 限值
时间周期	预测	SE 预测	下限	上限	实际
109	16.6381	0.0182964	16.6022	16.6739
110	16.8514	0.0184495	16.8153	16.8876
111	16.8516	0.0186014	16.8151	16.8880

使用最佳 ARIMA 模型进行预测 季节性模型的示例

解释结果

方法

模型选择

参数的最终估计值

模型汇总

修正 Box-Pierce(Ljung-Box) 卡方统计量

原始序列

已变换的序列

使用最佳 ARIMA 模型进行预测季节性模型的示例