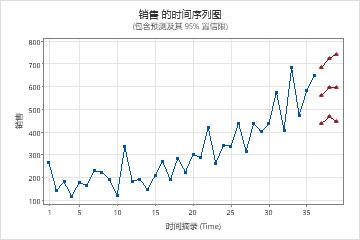
营销分析师希望使用 ARIMA 模型生成洗发水产品销售的短期预测。分析师收集前三年的销售数据。该分析人员之前检查了该序列的时间序列图和自相关函数 (ACF) 图。两个图都建议 1 作为非季节性差分顺序的起点。数据在时间序列图上不显示季节性模式,因此分析师选择从非季节性模型开始。分析师要求对未来 3 个月进行预测。
- 打开样本数据 洗发水的销售.MWX。
- 选择 。
- 在 序列中,输入销售。
- 在中差分阶次 d,选择 1。
- 取消选中模型中包括常量项。
- 在预测点数中,输入 3。
- 选择确定。
解释结果
模型选择表按 AICc 的顺序对搜索中的模型进行排名。ARIMA (0, 1, 2) 模型具有最少的 AICc。下面的 ARIMA 结果适用于 ARIMA (0, 1, 2) 模型。
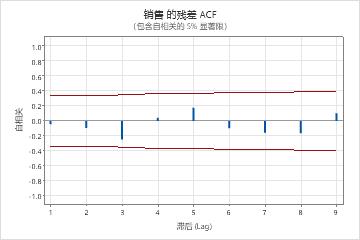
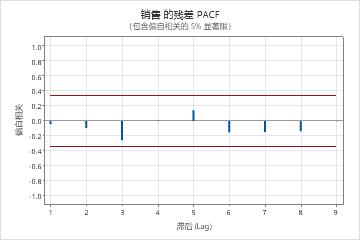
参数表中的 p 值显示移动平均线项在 0.05 水平上显著。分析人员得出结论,系数属于模型。修改后的箱形皮尔斯 (Ljung-Box) 统计量的 p 值在 0.05 水平上都是微不足道的。残差的 ACF 和残差的 PACF 均在各自图的 0.05 限制内。分析员得出模型符合残差保持独立这一假设。分析师的结论是,对预测的检查是合理的。
* 警告 * 不包含常量项的不可估计的 ARIMA(p, d, q) 模型:
(2, 1, 2)
方法
| 最佳模型的标准 | 最小 AICc |
|---|
| 已使用的行数 | 36 |
|---|
| 未使用的行 | 0 |
|---|
模型选择
| p = 0, q = 2* | -197.052 | 400.878 | 400.103 | 404.769 |
|---|
| p = 1, q = 2 | -196.989 | 403.311 | 401.978 | 408.199 |
|---|
| p = 1, q = 0 | -201.327 | 407.029 | 406.654 | 409.765 |
|---|
| p = 2, q = 0 | -200.239 | 407.251 | 406.477 | 411.143 |
|---|
| p = 1, q = 1 | -200.440 | 407.655 | 406.880 | 411.546 |
|---|
| p = 2, q = 1 | -201.776 | 412.884 | 411.551 | 417.773 |
|---|
| p = 0, q = 1 | -204.584 | 413.542 | 413.167 | 416.278 |
|---|
| p = 0, q = 0 | -213.614 | 429.350 | 429.229 | 430.784 |
|---|
参数的最终估计值
| MA 1 | 1.257 | 0.132 | 9.52 | 0.000 |
|---|
| MA 2 | -0.882 | 0.133 | -6.62 | 0.000 |
|---|
模型汇总
| 33 | 131017 | 3970.21 | 3743.34 | 400.878 | 400.103 | 404.769 |
|---|
修正 Box-Pierce(Ljung-Box) 卡方统计量
| 卡方 | 15.90 | 27.15 | * | * |
|---|
| 自由度 | 10 | 22 | * | * |
|---|
| P 值 | 0.103 | 0.206 | * | * |
|---|
* 警告 * 不包含常量项的不可估计的 ARIMA(p, d, q) 模型:
(2, 1, 2)
从时间周期 36 后开始的预测
|
| 95% 限值 |
|
|---|
| 37 | 563.193 | 63.0096 | 439.669 | 686.717 | |
|---|
| 38 | 594.912 | 65.0499 | 467.388 | 722.435 | |
|---|
| 39 | 594.912 | 76.0553 | 445.813 | 744.010 | |
|---|