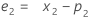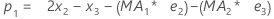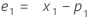模型方程
双指数平滑在每个周期处采用水平分量和趋势分量。双指数平滑使用两个权重(又称为平滑参数)在每个周期处更新分量。双指数平滑方程如下所示:
公式
Lt= αYt+ (1 – α) [Lt–1 + Tt–1]
Tt= γ [Lt – Lt–1] + (1 – γ) Tt–1
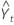 = Lt−1
+ Tt−1
= Lt−1
+ Tt−1
如果第一个观测值编号为一,则必须初始化时间零处的水平和趋势估计值才能继续。初始化方法用于确定如何以两种方式之一获取平滑值:使用最优权重或者使用指定的权重。
表示法
| 项 | 说明 |
|---|---|
| Lt | 时间 t 处的水平 |
| α | 水平的权重 |
| Tt | 时间 t 处的趋势 |
| γ | 趋势的权重 |
| Yt | 时间 t 处的数据值 |
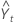 | 时间 t 处的预测值 |
权重
最优 ARIMA 权重
- Minitab 使用 ARIMA (0,2,2) 模型与数据拟合,以尽可能使误差平方和最小。
- 随后,向后预测方法对趋势和水平分量进行初始化。
指定的权重
- Minitab 将线性回归模型与时间序列数据(y 变量)和时间(x 变量)的关系进行拟合。
- 此回归中的常量是水平分量的初始估计值,斜率系数是趋势分量的初始估计值。
指定对应于等根 ARIMA (0, 2, 2) 模型的权重时,Holt 方法特殊化为 Brown 方法 1。
水平和趋势的初始值计算方法
可以存储水平和趋势的估计值。Minitab 根据您在对话框中指定的选项,使用以下方法之一来计算这些列第一行中的值。
如果您在 双指数平滑 中选择选项 最优综合自回归移动平均 (ARIMA),则 Minitab 使用以下方法来计算水平和趋势的第一个值。您可以手动执行这些步骤。
- 选择 以使用 ARIMA 计算最佳权重值。按照如下方式填写对话框:
- 在 自回归 中,输入 0。
- 在差值中,输入 2。
- 在移动平均中,输入 2。
- 取消选中 模型中包括常量项。
- 单击 存储,然后选中 残差。单击每个对话框中的确定。
- Minitab 使用 ARIMA 输出中的 MA 值来计算最优权重,如下所示:
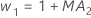
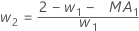
- 然后,Minitab 使用后续观测值的数据计算回初始观测值:
其中:
项 说明 pi 第 i 个平滑观测值的预测值 xi 时间序列中第 i 个观测值的值 ei 第 i 个残差的值,通过上面的 ARIMA 来存储 -
- Minitab 计算水平 (L1) 的初始值:

- Minitab 计算趋势的初始值 (T1):
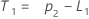
- 创建与时间序列数据列长度相等的时间索引列。从 1 到 n 的整数列就足够了。
- 选择 。
- 在 响应 中,输入时间序列数据列。在 连续预测变量 中,输入时间索引列。
- 单击 存储,然后选中 系数。单击每个对话框中的确定。
- 水平的初始值是:
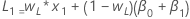
- 趋势的初始值是:
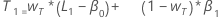 其中:
其中:项 说明 L1 水平的初始值 x1 时间序列中第一个观测值的值 T1 趋势的初始值 wL 水平的权重值 wT 趋势的权重值 β0 回归模型中的常量项的系数 β1 回归模型中的预测变量项的系数
预测
双指数平滑使用水平和趋势分量生成预测。对时间点 t 向前 m 个周期的预测为:
公式
Lt + mTt
预测原点时间之前的数据将用于进行平滑。
表示法
| 项 | 说明 |
|---|---|
| Lt | 时间 t 处的水平 |
| Tt | 时间 t 处的趋势 |
预测限
公式
- 上限 = 预测值 + 1.96 × dt × MAD
- 下限 = 预测值 – 1.96 × dt × MAD

表示法
| 项 | 说明 |
|---|---|
| β | max{α, γ) |
| δ | 1 – β |
| α | 水平平滑常量 |
| γ | 趋势平滑常量 |
| τ |  |
| b0(T) | 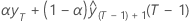 |
| b1(T) | 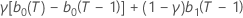 |
平均绝对百分比误差 (MAPE)
平均绝对百分比误差 (MAPE) 度量时间序列值拟合的准确度。MAPE 以百分比表示准确度。
公式
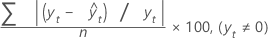
表示法
| 项 | 说明 |
|---|---|
| yt | 时间 t 处的实际值 |
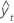 | 拟合值 |
| n | 观测值个数 |
平均绝对误差 (MAD)
平均绝对偏差 (MAD) 度量时间序列值拟合的准确度。MAD 以与数据相同的单位表示准确度,从而有助于使误差量概念化。
公式
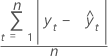
表示法
| 项 | 说明 |
|---|---|
| yt | 时间 t 处的实际值 |
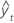 | 拟合值 |
| n | 观测值个数 |
平均偏差平方和 (MSD)
无论采用哪种模型,平均偏差平方和 (MSD) 始终是使用相同的分母 n 计算的。对于异常大的预测误差,MSD 度量比 MAD 敏感。
公式
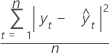
表示法
| 项 | 说明 |
|---|---|
| yt | 时间 t 处的实际值 |
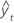 | 拟合值 |
| n | 观测值个数 |