请查找定义和解释指导，了解随互相关提供的每个统计量和图形。
滞后
滞后是指分隔两个时间序列的时间段数。默认滞后数的范围是 (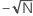
+ 10) 到 (
+ 10)。
互相关函数 (CCF)
互相关函数是两个时间序列 xt 和 yt 的观测值之间的相关，用 k 个时间单位分隔（yt+k 和 xt 之间的相关）。
解释
使用互相关函数可以确定两个时间序列之间是否存在关系。要确定两个序列之间是否存在关系，请查找较大的相关（即两端的相关迅速变得不显著）。通常，当绝对值大于 
（其中 n 是观测值个数，k 是滞后）时，存在显著相关。此计算是基于大样本正态近似的经验规则过程。如果滞后 k 的总体互相关为零（其中，k = 1,2 ...），那么对于相对较大的 n，rxy(k) 将近似正态分布，均值 (μ) 为零并且标准差 (σ) 为 1/
。由于正态总体的大约 95% 在均值的 2 倍标准差之内，因此，否定当 |rxy(k) | 大于 2/
时，滞后 k 的总体自相关等于零这一假设的检验所具有的显著性水平 (a) 约为 5%。
注意
互相关函数的解释取决于不存在互相关这一假设。有关更多信息，请转到查找自相关证据。
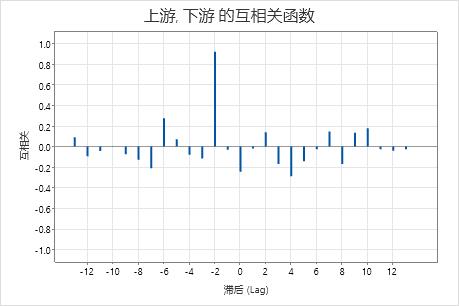
在该图中，滞后 −2 处的相关大约为 0.92。因为 0.92 > 0.5547 = 
，所以存在显著相关。您可以得出水在两天内从上游位置流到下游位置的结论。
