请查找定义和解释指导,了解随 Box-Cox 变换提供的每个统计量和图形。
方法表
方法表显示分析的设置和转换的 λ 值。
在这些结果中,季节性周期为 12,分析在默认范围 -1 和 2 之间搜索 λ 值。λ 的最优值约为 -0.15。分析将值舍入为 0,并使用自然对数转换。
方法
| 季节周期 | 12 |
|---|---|
| 从区间中选择最优 λ | [-1, 2] |
| 最优 λ | -0.144439 |
| 取整的最优 λ | 0 |
| 已变换的序列 = ln(乘客人数) |
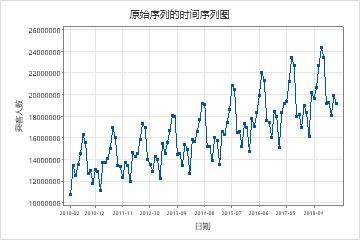
原始系列的时间序列图
将原始序列的时间序列与变换序列的时间序列图进行比较,以验证变换是否使方差静止。
在这些结果中,原始序列的时间序列图显示非平稳方差。在此数据中,季节性周期中的高点和低点之间的差异随着时间的推移而增加。此模式显示方差随着时间的推移而增加。
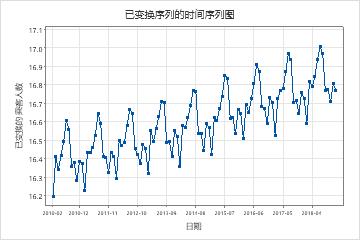
变换序列的时间序列图
检查变换序列的时间序列图,以验证变换是否使方差静止。
在这些结果中,变换序列的时间序列图显示了季节周期中高点和低点之间的近似均匀差异。此模式表明变换使方差静止。
还要检查变换数据的时间序列图,以评估变换序列的其他重要特征。例如,ARIMA 模型的假设包括,除了平稳方差之外,序列还具有平稳均值。如果变换序列的时间序列图显示变换序列没有平稳均值,请尝试 增强的 Dickey-Fuller 检验 查看数据的差异是否使序列的均值静止。
在这些结果中,变换后的序列显示出上升趋势。此模式表明序列的均值不是平稳的。使用 已 增强的 Dickey-Fuller 检验 转换数据的存储列上的 可确定差异是否使序列保持平稳。