回归模型
| 项 | 说明 |
|---|---|
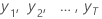 | 时间处观察到的时间序列值 = 1, ..., T |
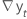 | 时间 t 处两个连续观测值的差 t, 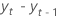 ,其中 t = 2,..., T ,其中 t = 2,..., T |
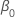 | 回归模型中的常量项 |
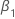 | 回归模型中线性时间趋势的系数 |
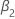 | 回归模型中二次时间趋势的系数 |
 | 自回归过程的滞后顺序 |
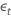 | 时间 t= 2 , ..., T时的序列独立误差项 |
- 只有常数系数的模型

- 具有恒定系数和线性系数的模型
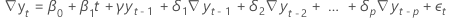
- 具有常数系数、线性系数和二次系数的模型

- 没有回归系数的模型
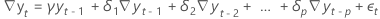
假设
每个增强型 Dickey-Fuller 检验都使用以下假设:
原假设,H0:
备择假设,H1:
原假设表示单位根位于时间序列样本中,这意味着数据的平均值不是平稳的。否定原假设表示数据的均值是平稳的或趋势平稳的,具体取决于检验的模型。
检验统计量
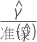
其中,
| 项 | 说明 |
|---|---|
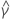 | 的最小二乘系数估计 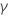 系数 系数 |
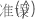 | 最小二乘估计的标准误差 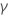 回归模型中的系数 回归模型中的系数 |
麦金农的近似 p 值
在原假设下,检验统计量的渐近分布不遵循标准分布。富勒 (1976)1 提供了一个包含渐近分布的公共百分位数的表。麦金农 (19942, 2010MacKinnon3) 将响应面近似应用于模拟数据,以便为 ADF 检验统计量的任何值提供近似 p 值。
如果分析的规范使用 0.01、0.05 或 0.1 作为显著性水平,则原假设的评估会将检验统计量与该显著性水平的临界值进行比较。如果检验统计量小于或等于临界值,则否定原假设。
如果分析的规范给出了不同的显著性水平,则原假设的计算会将近似 p 值与显著性水平进行比较。如果 p 值小于显著性水平,则否定原假设。
显著性水平 0.01、0.05 和 0.1 的临界值
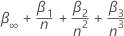
其中 n 是分析用于拟合回归模型的观测值数。的值 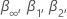 和
和 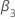 来自MacKinnon(2010)中的表格。如果检验统计量小于或等于临界值,则否定原假设。
来自MacKinnon(2010)中的表格。如果检验统计量小于或等于临界值,则否定原假设。
近似 p 值
近似p值的计算来自Mackinnon(1994)。将 p 值与显著性水平进行比较以做出决定。如果 p 值小于或等于显著性水平,则否定原假设。
确定滞后顺序
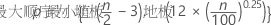
滞后顺序的选择取决于分析规范中的标准。如果分析的规范不包含条件,则检验的回归模型是 p 的最大阶 数。
在确定滞后顺序的计算中,观测值的数量取决于最大滞后顺序,使得 m = n – p – 1。
| 项 | 说明 |
|---|---|
| n | 观测值总数 |
| p | 模型中差分项的最大滞后顺序 |
每个标准的计算如下:
Akaike 信息准则 (AIC)
该分析将评估分析规范中每个滞后顺序的回归模型。测试的滞后顺序是具有 AIC 最小值的回归模型。
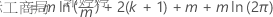
其中,
| 项 | 说明 |
|---|---|
| m | 取决于最大滞后顺序的观测值数 |
| k | 模型中的系数数,包括回归模型中非零常量时的常量 |
| 郭婷婷 | 回归模型的残差平方和 |
贝叶斯信息准则 (BIC)
该分析将评估分析规范中每个滞后顺序的回归模型。测试的滞后顺序是具有 BIC 最小值的回归模型。
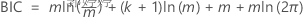
其中,
| 项 | 说明 |
|---|---|
| m | 取决于最大滞后顺序的观测值数 |
| k | 模型中的系数数,包括回归模型中非零常量时的常量 |
| 郭婷婷 | 回归模型的残差平方和 |
t 统计量

其中 i = 1, ..., p
| 项 | 说明 |
|---|---|
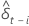 | 的最小二乘估计  回归模型中的系数 回归模型中的系数 |
 | 最小二乘估计的标准误差  回归模型中的系数 回归模型中的系数 |
