营销分析师希望使用 ARIMA 模型生成洗发水产品销售的短期预测。分析师收集前三年的销售数据。在时间序列图上,分析师看到数据呈上升趋势。此模式指示数据的均值不是平稳的。该分析器执行增强的 Dickey-Fuller 检验,以确定要包含在 ARIMA 模型中的非季节性差异的顺序。有关 ARIMA 型号的详细信息,请转至 综合自回归移动平均 (ARIMA) 的概述。
- 打开样本数据 洗发水的销售.MWX。
- 选择 。
- 在序列中,输入销售。
- 选择确定。
解释结果
在这些结果中,检验统计量 2.29045 大于临界值 -2.96053。由于结果无法否定数据为非平稳的原假设,因此检验的建议是考虑一阶差分以使数据平稳。
方法
| 回归模型中项的最大滞后阶数 | 9 |
|---|---|
| 滞后阶数的选择标准 | 最小 AIC |
| 其他项 | 常量 |
| 选定的滞后阶数 | 4 |
| 已使用的行数 | 36 |
增强的 Dickey-Fuller 检验
| 原假设: | 数据不稳定 |
|---|---|
| 备择假设: | 数据稳定 |
| 检验统计量 | P 值 | 建议 |
|---|---|---|
| 2.29045 | 0.999 | 检验统计量 > -2.96053 的临界值。 |
| 显著性水平 = 0.05 | ||
| 未能否定原假设。 | ||
| 考虑进行差值处理以使数据保持稳定。 |
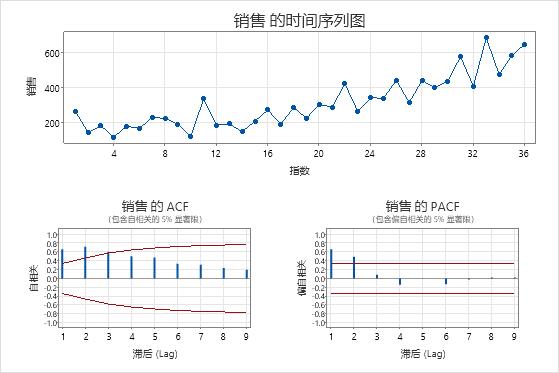
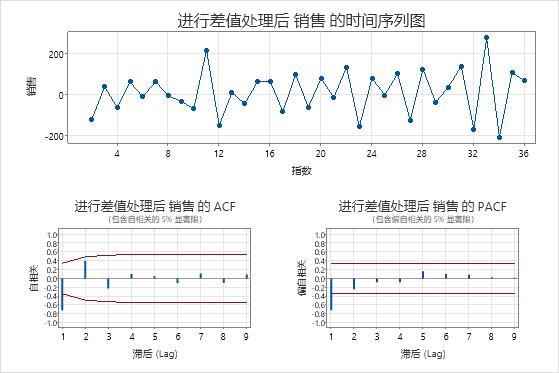
时间序列图显示差异的结果。在这些结果中,原始数据的时间序列图显示了明显的趋势。差分数据的时间序列图显示连续值之间的差异。差分数据显示为静止,因为点沿水平路径,变体中没有明显的模式。
ACF 图还显示了差分的影响。在这些结果中,原始数据的 ACF 图显示了跨滞后的缓慢下降的峰值。此模式表示数据不是静止的。在差分数据的 ACF 图中,唯一与 0 显著不同的峰值滞后为 1。
在这些结果中,时间序列图和 ACF 图确认测试结果。因此,一种合理的方法是对数据进行差异化,然后拟合自回归和移动平均模型进行预测。
基于这些结果,分析师计划探索具有 1 阶差分的 ARIMA 模型。在某些情况下,差分数据的ACF和PACF图中的模式表明了要包含在ARIMA模型中的自回归项和移动平均项的顺序。有关这些图的解释的详细信息,请转到以下主题: