时间序列图
时间序列图按时间顺序显示数据。生成预测时,Minitab 在图中显示预测及其 95% 置信限。
解释
- 确定数据中是否存在不同的变异。如果存在不同的变异,则必须转换数据,以便方差恒定。
- 确定数据是否集中在恒定的均值周围。如果均值不恒定,您可能需要对数据进行差分以使均值恒定。
残差的 ACF
该图显示残差的自相关函数。自相关函数用来度量时间序列中每隔 k 个时间单位(yt 和 yt–k)的观测值之间的相关。
解释
使用残差的自相关函数可以确定模型是否符合残差保持独立这一假设。如果未满足此假设,则模型可能无法拟合数据,在解释结果时应当格外小心。如果不存在显著的相关,则可以得出残差独立的结论。但是,在较高阶的非季节性滞后处,您可能会看到 1 个或 2 个显著相关。这些滞后通常是由随机误差引起的,它们并不说明未满足假设。因此,在这种情况下,您也可以得出残差保持独立的结论。
残差的 PACF
偏自相关函数用来度量暂时调整所有其他较短滞后的项 (yt–1, yt–2, ..., yt–k–1) 之后,时间序列中每隔 k 个时间单位(yt 和 yt–k)的观测值之间的相关。
解释
使用残差的偏自相关函数可以确定模型是否符合残差保持独立这一假设。如果未满足此假设,则模型可能无法拟合数据,在解释结果时应当格外小心。如果不存在显著的相关,则可以得出残差独立的结论。
残差的直方图
残差的直方图显示所有观测值的残差的分布情况。如果模型与数据很好地拟合,则残差应当随机分布且均值为 0。因此,直方图应当相对于 0 大致对称。
残差的正态概率图
残差的正态图显示当分布服从正态时残差与期望值的关系。
解释
使用残差的正态图可以确定残差是否呈正态分布。但是,此分析不要求残差呈正态分布。
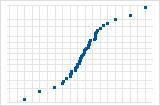
S 曲线表示长尾分布。
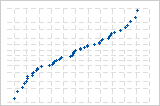
反向 S 曲线表示短尾分布。
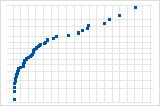
向下的曲线表示右偏斜分布。
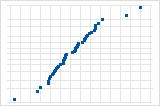
远离线的几个点表示分布中有异常值。
残差与拟合值
残差与拟合图在 y 轴上显示残差,在 x 轴上显示拟合值。
解释
使用残差与拟合值的关系图可以确定残差是否不偏斜且具有恒定的方差。理想情况是,点应当随机落在两端(0 处),点中没有可识别的模式。
| 模式 | 模式的含义 |
|---|---|
| 残差相对拟合值呈扇形或不均匀分散 | 异方差 |
| 曲线 | 缺少高次项 |
| 远离 0 的点 | 异常值 |
如果您在残差中看到非恒定的方差或模式,则说明预测值可能不准确。
残差与顺序
残差与顺序的关系图按照数据的收集顺序显示残差。
解释
使用残差与顺序的关系图可以确定在观测期间内,拟合值相对于观测值的准确度。点中的模式可能指示模型与数据不拟合。理想情况是,图上的残差应围绕中心线随机分布。
| Pattern | 模式的含义 |
|---|---|
| 一致的长期趋势 | 模型与数据不拟合 |
| 短期趋势 | 模式中的偏移或变化 |
| 远离其他点的点 | 异常值 |
| 点中的突然偏移 | 数据的基础模式已改变 |
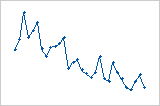
随着观测值的顺序从左到右提高,残差以系统方式降低。
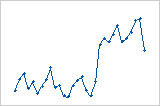
残差的值从低(左)到高(右)突然变化。
残差与变量
残差与变量的关系图显示残差与另一个变量的关系。
解释
使用该图可以确定变量是否会以系统方式对响应造成影响。如果残差中存在模式,则说明其他变量与响应相关联。您可以使用此信息作为其他研究的基础。
