就业分析员对五年(60 个月)间三个行业的就业趋势进行了研究。分析员执行 ARIMA 以拟合贸易行业的模型。
- 打开样本数据 就业趋势.MWX。
- 选择。
- 在 序列中,输入交易。
- 在自回归中的非季节下面,输入 1。
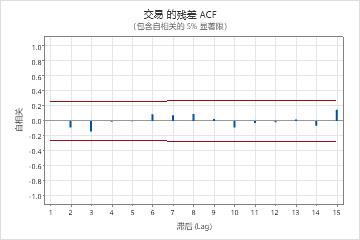
- 单击图形,然后选择残差的 ACF。
- 单击确定。
解释结果
自回归项的 p 值小于显著性水平 .0.05。分析员得出自回归项的系数在统计意义上不同于 0 的结论并将该项保留在模型中。Ljung-Box 卡方统计量的 p 值均大于
.0.05,残差的自相关函数的任何相关都不显著。分析员得出模型符合残差保持独立这一假设。
每次迭代的估计值
| 迭代 | SSE | 参数 | |
|---|---|---|---|
| 0 | 543.908 | 0.100 | 90.090 |
| 1 | 467.180 | -0.050 | 105.068 |
| 2 | 412.206 | -0.200 | 120.046 |
| 3 | 378.980 | -0.350 | 135.024 |
| 4 | 367.545 | -0.494 | 149.372 |
| 5 | 367.492 | -0.503 | 150.341 |
| 6 | 367.492 | -0.504 | 150.410 |
| 7 | 367.492 | -0.504 | 150.415 |
参数的最终估计值
| 类型 | 系数 | 系数标准误 | T 值 | P 值 |
|---|---|---|---|---|
| AR 1 | -0.504 | 0.114 | -4.42 | 0.000 |
| 常量 | 150.415 | 0.325 | 463.34 | 0.000 |
| 均值 | 100.000 | 0.216 |
观测值个数: 60
残差平方和
| 自由度 | SS | MS |
|---|---|---|
| 58 | 366.733 | 6.32299 |
修正 Box-Pierce(Ljung-Box) 卡方统计量
| 滞后 (Lag) | 12 | 24 | 36 | 48 |
|---|---|---|---|---|
| 卡方 | 4.05 | 12.13 | 25.62 | 32.09 |
| 自由度 | 10 | 22 | 34 | 46 |
| P 值 | 0.945 | 0.955 | 0.849 | 0.940 |

