使用 Weibull 分布可以对可靠性数据建模
Weibull 分布是最常用于对可靠性数据建模的分布。此分布易于解释且用途广泛。在可靠性分析中,可以使用此分布回答以下问题:
- 预计将在老化期间失效的项目所占的百分比是多少?例如,预计将在 8 小时老化期间失效的保险丝占多大百分比?
- 预计在有效寿命阶段有多少次保修索赔?例如,在该轮胎的 50,000 英里有效寿命期间预计有多少次保修索赔?
- 预计何时会出现快速磨损?例如,应将维护定期安排在何时以防止发动机进入磨损阶段?
Weibull 分布可以对右偏斜数据、左偏斜数据或对称数据建模。因此,分布可用来评估不同应用(包括真空管、电容器、滚珠轴承、继电器和材料强度)的可靠性。Weibull 分布还可以对递增、递减或固定故障函数建模,并允许使用该模型描述项目寿命的任何阶段。
Weibull 分布可能不适用于由化学反应或退化过程(如半导体失效时出现的腐蚀)造成的产品失效。通常会使用对数正态分布对这些情况建模。
- Rayleigh 分布
- 当 Weibull 分布的形状参数为 2 时,它被称为 Rayleigh 分布。此分布通常用来描述通信工程领域中的测量数据,如输入回波损耗、调制边带注入、载波抑制和 RF 衰减的测量数据。此分布还广泛用于电真空设备的寿命检验中。
- 最弱环节模型
- Weibull 分布还可以对具有多个导致失效的、相同且独立的过程的寿命分布建模,其中第一个到达关键阶段的过程决定失效时间。极值理论可以用作此“最弱环节”模型的基础,其中许多瑕疵都可能是失效的真正原因。由于 Weibull 分布理论上可以从最小极值分布中得出,因此,也可以为最弱环节应用(如电容器、滚珠轴承、继电器以及材料强度的失效)提供有效模型。但是,如果相关变量可以取负值,则最小极值分布就更适合,因为 Weibull 分布只可以对正值建模(其下限为 0)。
示例 1:电容器
在高应力下检验电容器以获得失效数据(用小时数表示)。使用 Weibull 分布对失效数据建模。
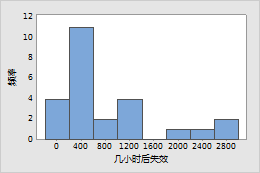
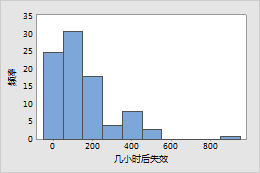
示例 2:灯丝
一家灯泡公司制造的白炽灯丝预计在正常使用期限之后不会出现耗损。这家公司的工程师希望保证灯泡正常使用 10 年。他们给灯泡施加应力以模拟长期使用情况并记录每个灯泡在使用多长时间之后失效。
Weibull 分布参数、可靠性函数和故障函数之间的关系
通过调整 Weibull 分布的形状参数 β,可以对许多不同寿命分布的特征建模。
0 < ß < 1
早期失效发生在产品寿命的初始阶段。这些失效可能会迫使产品进入“老化”阶段以降低初期失效的风险。
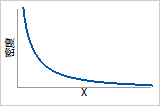

概率密度函数
从无穷远处成指数递减

故障函数
初始失效率很高,随着时间的推移会逐渐降低(“浴盆”形状故障函数的第一部分)
ß = 1
失效率保持恒定。随机失效,失效的原因有多种。对产品的“使用寿命”建模。
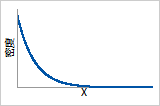


概率密度函数
从 1/α(α = 尺度参数)处成指数递减

故障函数
失效率在产品寿命期间保持恒定(“浴盆”形状故障函数的第二部分)
ß = 1.5
早期磨损失效
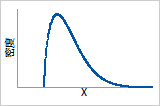

概率密度函数
增加到峰值,之后减小

故障函数
失效率不断增加,最初增加速度最快
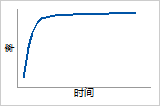
ß = 2
在产品的寿命期间,磨损失效风险不断增加
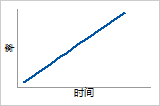

概率密度函数
Rayleigh 分布

故障函数
失效率呈线性增加
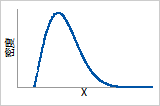
3 ≤ ß ≤4
快速磨损失效。当大多数的失效都出现后,对产品寿命的最后时间段建模。
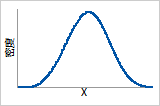
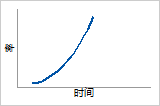

概率密度函数
钟形

故障函数
快速增加
ß > 10
非常快的磨损失效。当大多数的磨损失效都出现后,对产品寿命的最后时间段建模。
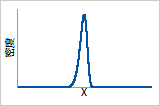

概率密度函数
与极值分布相似

故障函数
增加速度非常快
