使用指数分布可以对可靠性数据建模
指数分布是只有一个参数的简单分布,通常用于对可靠性数据建模。指数分布实际上是 Weibull 分布在 ß = 1 时的特殊情况。
如果产品或项目在任意时间(无论是崭新、用了一年还是用了多年)都有可能失效,则指数分布可为产品的阶段或者项目的寿命提供很好的模型。换句话说,对在产品的预期应用期间产品开始老化和磨损之前的阶段进行建模。
- 如果电子元件在装有它的产品的预期寿命之后很长时间通常都不磨损,则往往使用指数分布对这些电子元件进行建模。示例包括优质集成电路的元件(如二极管、晶体管、电阻器和电容器)。
- 对于长期“扁平”(相对固定)的低失效风险期(体现了浴盆曲线的中间部分),指数分布被视为优异的模型。此阶段对应于产品的有用寿命,被称为曲线的“内在失效”部分。
- 但是,对于在产品的预期寿命结束之前预计将表现为疲劳、腐蚀或磨损的机械或电子元件,不应当使用指数分布进行建模。
指数分布的重要属性为它是无记忆的。无记忆属性指示元件的剩余寿命与其当前使用年限无关。例如,经过磨损并在使用年限后期更容易失效的系统便不是无记忆的。因此,当失效率在产品的整个寿命期间保持固定不变时,应当使用指数分布。每个时间单位的失效数通常表示为每个单位时间的失效百分比,例如,每一千个小时中的失效百分比。
示例 1:晶体管
已知电子元件的失效率在产品的预期寿命期间保持固定不变。工程师记录在正常操作条件下元件的失效时间。
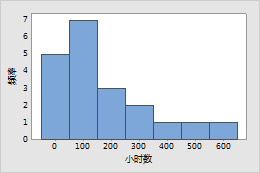
示例 2:灯丝
一家灯泡公司制造的白炽灯丝预计在正常使用期限之后不会出现耗损。工程师希望保证灯泡正常使用 10 年。他们给灯泡施加应力以模拟长期使用情况并记录每个灯泡在使用多长时间之后失效。
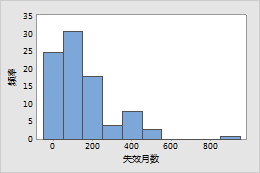
指数分布的概率密度函数和故障函数
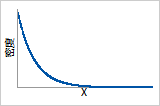
概率密度函数
概率密度函数显示失效数据向右偏斜

故障函数
故障函数显示失效风险保持固定不变
