一位可靠性工程师想预测因有缺陷的冰箱压缩机而导致的保证索赔。工程师收集和分析去年的每月失效数据。
工程师知道将来的生产计划是每月运输 1000 台设备。可以使用 Weibull 分布对失效数据进行建模。在重新设置预处理保证数据的格式之后,工程师使用保证预测来预测将来的保证索赔。
- 打开样本数据,压缩机失效_预处理.MWX。
- 选择。
- 在起始时间中,输入起始时间。
- 在结束时间中,输入结束时间。
- 在频率(可选)中,输入频率。
- 单击预测。在每个时间周期的生产数量中,输入 1000。
- 在每个对话框中单击确定。
解释结果
“当前保证索赔摘要”表中的结果指示,在数据收集阶段,现场的 12,000 个压缩机中,有 69 个压缩机失效。根据使用 Weibull 分布获得的估计值,预计大约有 69 个压缩机在这段时间内失效。
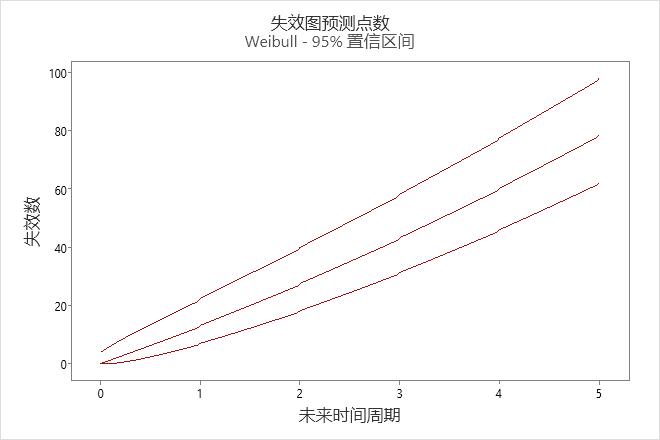
使用预测失效数表和预测失效数图,工程师以 95% 的置信度断定,预计在接下来的五个月内失效的额外压缩机数量位于大约 62 到 98 个压缩机这一区间内。
使用 频率 中的频率
分布参数
| 分布 | 形状参数 | 尺度 |
|---|---|---|
| Weibull | 1.26494 | 398.062 |
当前保证索赔的摘要
| 单位总数 | 12000 |
|---|---|
| 故障函数 | 69 |
| 期望的失效数 | 68.5201 |
| 95% Poisson 置信区间 | (53.2630, 86.7876) |
| 未来时间周期故障的单位数 | 11931 |
生产计划
| 未来时间周期 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 产品质量 | 1000 | 1000 | 1000 | 1000 | 1000 |
失效的预测数表
| 95% Poisson 置信区间 | ||||
|---|---|---|---|---|
| 未来时间周期 | 潜在失效数 | 失效预测点数 | 下限 | 上限 |
| 1 | 12931 | 13.1073 | 7.0000 | 22.3660 |
| 2 | 13931 | 27.4930 | 18.1933 | 39.8678 |
| 3 | 14931 | 43.1798 | 31.2722 | 58.1271 |
| 4 | 15931 | 60.1892 | 45.9516 | 77.4449 |
| 5 | 16931 | 78.5416 | 62.1373 | 97.9488 |