工程师希望评估经过重新设计的喷气发动机压缩机外壳的可靠性。为了检验此设计,工程师使用一台机器向每个压缩机外壳抛出一个弹射体。在经过弹射体冲击后,工程师每 12 小时检查压缩机是否存在故障。
工程师执行寿命数据回归,以评估外壳设计、弹射体重量、故障时间之间的关系。他们还想要估计在预期 1% 和 5% 的发动机失败时发生的故障次数。工程师使用 Weibull 分布来建模数据。
- 打开样本数据,喷气发动机可靠性.MWX。
- 选择。
- 选择响应为非删失/任意删失数据。
- 在变量/初始变量中,输入起始。
- 在结尾变量中,输入结束。
- 在模型中,输入设计和重量。
- 在因子(可选)中,输入设计。
- 单击估计。在输入新的预测变量值中,输入新设计新重量。
- 在估计下列百分比的百分位数中,输入 1 5,然后单击确定。
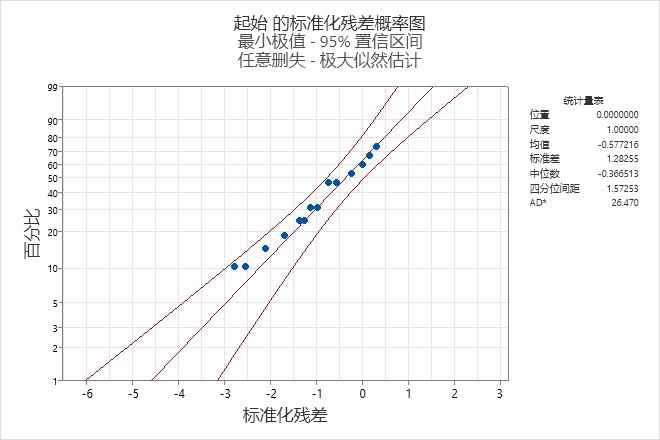
- 单击图形。选择标准化残差的概率图。
- 在每个对话框中单击确定。
解释结果
在回归表中,设计和重量的 p 值在 α 水平 0.05 处显著。因此,工程师断定,机箱设计和抛射物重量均对失效时间造成统计意义上显著的效应。预测变量的系数可用来定义描述机箱设计、抛射物重量和发动机失效时间之间关系的方程。
百分位数表显示每个机箱设计和抛射物重量组合的第 1 个和第 5 个百分位数。在所有抛射物重量下,与标准机箱设计相比,新机箱设计在 1% 或 5% 的发动机失效之前经过的时间更长。例如,在受到 10 磅抛射物的冲击之后,具有标准机箱设计的发动机中有 1% 预计会在大约 101.663 小时之后失效。而对于新机箱设计来说,大约有 1% 的发动机预计会在大约 205.882 小时之后失效。
标准化残差的概率图显示点沿着近似的直线分布。因此,工程师可以假设模型是合适的。
响应变量初始:起始 结束: 结束
删失
| 删失信息 | 计数 |
|---|---|
| 右删失值 | 25 |
| 区间删失值 | 23 |
估计法:极大似然
分布: Weibull
与加速变量的关系: 线性
回归表
| 95.0% 正态置信区间 | ||||||
|---|---|---|---|---|---|---|
| 自变量 | 系数 | 标准误 | Z | P | 下限 | 上限 |
| 截距 | 6.68731 | 0.193766 | 34.51 | 0.000 | 6.30754 | 7.06709 |
| 设计 | ||||||
| 标准 | -0.705643 | 0.0725597 | -9.72 | 0.000 | -0.847857 | -0.563428 |
| 重量 | -0.0565899 | 0.0212396 | -2.66 | 0.008 | -0.0982187 | -0.0149611 |
| 形状 | 5.79286 | 1.07980 | 4.02001 | 8.34755 | ||
对数似然 = -88.282
Anderson-Darling(调整)拟合优度检验
标准化残差 = 26.470
百分位数表格
| 95.0% 正态置信区间 | ||||||
|---|---|---|---|---|---|---|
| 百分比 | 设计 | 重量 | 百分位数 | 标准误 | 下限 | 上限 |
| 1 | 标准 | 5.0 | 134.911 | 17.6574 | 104.385 | 174.363 |
| 1 | 标准 | 7.5 | 117.113 | 16.0279 | 89.5591 | 153.144 |
| 1 | 标准 | 10.0 | 101.663 | 16.3830 | 74.1295 | 139.423 |
| 1 | 新品牌 | 5.0 | 273.214 | 36.8022 | 209.819 | 355.763 |
| 1 | 新品牌 | 7.5 | 237.171 | 32.6878 | 181.028 | 310.726 |
| 1 | 新品牌 | 10.0 | 205.882 | 32.8675 | 150.568 | 281.518 |
| 5 | 标准 | 5.0 | 178.749 | 16.9676 | 148.404 | 215.300 |
| 5 | 标准 | 7.5 | 155.168 | 14.1107 | 129.836 | 185.443 |
| 5 | 标准 | 10.0 | 134.698 | 15.4568 | 107.568 | 168.670 |
| 5 | 新品牌 | 5.0 | 361.994 | 36.0778 | 297.761 | 440.084 |
| 5 | 新品牌 | 7.5 | 314.239 | 28.8741 | 262.450 | 376.247 |
| 5 | 新品牌 | 10.0 | 272.783 | 30.6102 | 218.928 | 339.887 |