给定百分比的百分位数的点估计
第 p个 百分位点 xp是响应 p所需的应力水平。
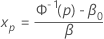
要找到 xp的估计值,请使用以下公式:
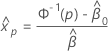
其中,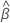 和
和 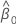 是
是  和
和 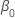 。
。
概率单位分析的对数位置分布包括对数正态分布、对数 Logistic 分布和 Weibull 分布。对于对数位置分布,前面的公式估计了对数刻度上的百分位数。要估计具有这些分布的数据尺度的百分位数,请使用以下公式。
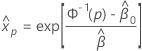
给定百分比的百分位数标准误
百分位数标准误差的计算使用 delta 方法。估计百分位数的标准误具有以下公式。

其中  具有以下形式:
具有以下形式:
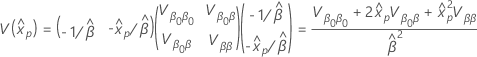
以及 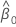 和
和 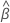 具有以下形式:
具有以下形式:
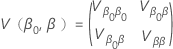
概率单位分析的对数位置分布包括对数正态分布、对数 Logistic 分布和 Weibull 分布。对于对数位置分布,前面的公式估计 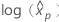 。方差和方差-协方差矩阵的定义
。方差和方差-协方差矩阵的定义 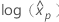 跟随。
跟随。
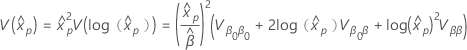

给定百分比的百分位数的基准置信区间
双面,100(1 -  ) 为
) 为  是
是 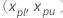 替换为以下方程。
替换为以下方程。
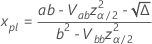
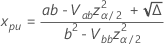
其中
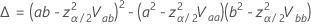
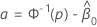

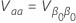


概率单位分析的对数位置分布包括对数正态分布、对数 Logistic 分布和 Weibull 分布。对于对数位置分布,前面的公式估计对数刻度上的间隔。要估计数据尺度上的区间,请对前面公式中的置信限取指数。
给定应力值下的失效概率或生存概率的基准置信区间
双面,100(1 -  ) 的故障概率,
) 的故障概率, 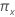 是
是  。对于生存概率,
。对于生存概率,  ,则区间为
,则区间为 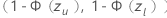 。以下公式给出了计算结果。
。以下公式给出了计算结果。
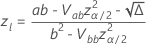
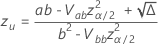
其中
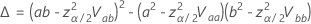


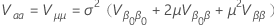

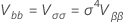
并且 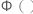 是分析分布的累积分布函数。
是分析分布的累积分布函数。
概率单位分析的对数位置分布包括对数正态分布、对数 Logistic 分布和 Weibull 分布。对于日志位置分布,请替换以下定义。

参考资料
基准置信区间的推导使用 Fieller 定理。Fieller 定理位于以下参考文献中。
Finney, D. J. (1971). Probit analysis, (Third edition), London: Cambridge University Press.
有关 probit 模型和百分位数估计的更多信息,请参阅以下参考资料。
Cox, D. R. and Snell, E. J. (1989). The analysis of binary data (Second edition), London: Chapman & Hall.
