累积失效函数均值 (MCF) 图显示累积失效函数均值与时间的关系。使用此图可以确定系统正在改善、恶化还是保持不变。
该图包括下列各项:
- 借助于经验累积失效函数均值的 Nelson-Aalen 方法计算的标绘点。标绘点不假定特定模型。当您具有区间数据时,Minitab 将通过在每个区间内均匀分布发生次数并绘制相应点来估计失效时间。
- 基于估计的分布形状和尺度的累积失效函数均值。对于幂律过程,系统失效率可以增大、减小或保持不变。生成的图形可以是直线或上凹或下凹的曲线。对于齐次 Poisson 过程,失效率为常量,因而生成一条直线。
要评估分布模型的拟合优度,请检查标绘点与直线或曲线的距离。如果点紧密分布在直线或曲线附近,则说明分布能够提供很好的拟合。
MCF 图还提供有关系统失效模式的信息:
- 直线表示系统失效在一段时间内保持不变 - 系统稳定。
- 下凹曲线表示失效间隔时间随时间推移而增加 - 系统可靠性得到改善。
- 上凹曲线表示失效间隔时间随时间推移而减小 - 系统可靠性在不断恶化。
您可能要将最小 X 尺度值设置为第一次失效的时间,以便更轻松地查看失效率。
注意
由于 Nelson-Aalen 图不依赖于模型,因此无论您选择哪种估计方法和模型类型,标绘点都相同。但是,累积失效函数均值图会因模型而异。
输出示例
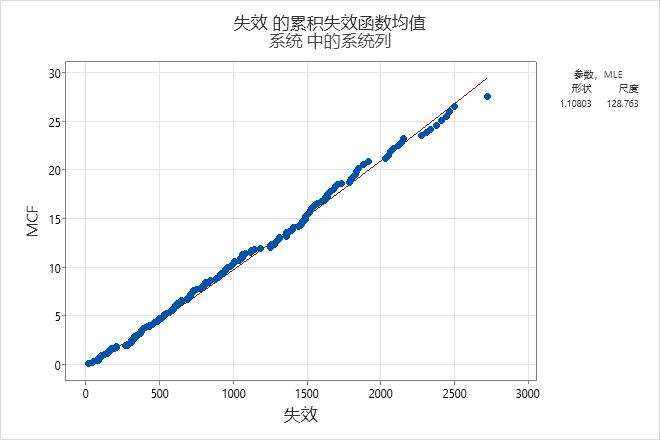
解释
对于空调数据,累积失效函数均值的估计大致是线性的,这表示系统失效率相对稳定。
