概率图
概率图包括以下内容:
- 标绘点,它们是顺序数据集的对应概率的估计百分位数。
- 拟合线,它们是从基于极大似然参数估计值的分布得到的预期百分位数。
- 置信区间,它们是百分位数的置信区间。
由于标绘点并不依赖于任何分布,因此它们对于所生成的任意概率图都是一样的(变换前)。但是,拟合线会因所选参数分布的不同而不同。因此您可以使用概率图来评估某个特定分布是否与您的数据拟合。通常,点越接近拟合线,表明拟合得越好。
标绘点
概率图的标绘点表示产品在时间 t 之前失效的似然性。对于右删失或非删失数据,Minitab 使用以下方法计算标绘点:
- 中位数秩方法(默认)
- 修正后 Kaplan-Meier 方法
- Herd-Johnson 方法
- Kaplan-Meier 方法
如果数据中包含结失效时间(相同的失效时间),则将绘制所有点(默认)、平均值(中位数)或最大结点数。如果结涉及到失效和延期,则会认为失效发生在延期之前。
这些方法中的每一种方法都生成 F(t) 的非参数估计值、随机变量 T(失效时间)的累积分布函数。
对于包含 n 个观测值的样本,假设 x(1), x(2),...,x(n) 为顺序统计量或者按从小到大排序的数据。因此,i 是第 I 个排序观测值 x(I) 的秩。每种方法的公式如下:
中位数秩(Benard 方法)
非删失数据的公式
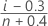
删失数据的公式

修正后 Kaplan-Meier
非删失数据的公式
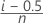
删失数据的公式
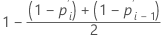
Herd-Johnson 估计值
非删失数据的公式

删失数据的公式
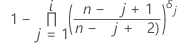
Kaplan-Meier 乘积限估计值
注意
如果最大的观测值是非删失数据,则 Kaplan-Meier 方法会为最大的非删失观测值生成 p = 1。在这种情况下,最大观测值的 Kaplan-Meier 估计值会生成一个无法用在图中的数字。此问题可通过重新计算最大 p(等于先前 p 和 1 之间距离的 90%)来更正。
注意
对于任意删失数据,Minitab 使用 Turnbull 方法估计累积概率1。
非删失数据的公式

删失数据的公式
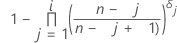
表示法
| 项 | 说明 |
|---|---|
| ii | 具有结的数据点的秩(假设为连续秩) |
| n | 数据中的观测值个数 |
| δj | 0(如果第 j 个观测值是删失的)或 1(如果第 j 个观测值是非删失的) |
| ARi |
 |
| AR0 | 等于 0 |
| p'i |
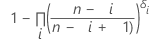 |
拟合线
下表显示拟合线的 x 和 y 坐标的构造方式。请注意以下几点:
- 当您使用 Weibull、3 参数 Weibull、指数、对数正态或对数 Logistic 分布时,Minitab 将 x 轴变换为对数尺度。
- 在默认情况下,Minitab 将 y 轴变换为百分比尺度。如果您将 y 尺度类型更改为概率,Minitab 会将 y 轴更改为概率尺度。
| 分布 | x 坐标 | y 坐标 |
|---|---|---|
| 最小极值 | 失效时间 | ln(–ln(1 – p)) |
| Weibull | ln(失效时间) | ln(–ln(1 – p)) |
| 3 参数 Weibull | ln(失效时间 – 阈值) | ln(–ln(1 – p)) |
| 指数 | ln(失效时间) | ln(–ln(1 – p)) |
| 双参数指数 | ln(失效时间 – 阈值) | ln(–ln(1 – p)) |
| 正态 | 失效时间 | Φ –1 (p) |
| 对数正态 | ln(失效时间) | Φ –1 (p) |
| 3 参数对数正态 | ln(失效时间 – 阈值) | Φ –1 (p) |
| Logistic | 失效时间 |
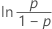 |
| 对数 Logistic | ln(失效时间) |
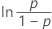 |
| 3 参数对数 Logistic | ln(失效时间 – 阈值) |
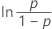 |
表示法
| 项 | 说明 |
|---|---|
| Φ –1 | 标准正态分布的逆 CDF |
| ln (x) | x 的自然对数 |
1 B.W. Turnbull (1976)。“The Empirical Distribution Function with Arbitrarily Grouped, Censored and Truncated Data”(具有任意分组、删失和截尾数据的经验分布函数),Journal of the Royal Statistical Society(皇家统计学会杂志),第 38 期,第 290-295 页。
