概率图
使用概率图可评估所选分布对数据的拟合程度。如果点紧密地沿着拟合线分布,则可以假定分布对数据的拟合相当好。
- 图上的点是基于非参数方法的估计百分位数(不依赖于任何分布)。将指针放在某个数据点时,Minitab 将显示观测到的失效时间和估计的累积概率。
- 拟合线(中心线)基于拟合分布。将指针放在拟合线上时,Minitab 将显示一个包含各种百分比的百分位数表。
- 左侧的线连接每个百分位数的置信区间下限。右侧的线连接每个百分位数的置信区间上限。
示例输出
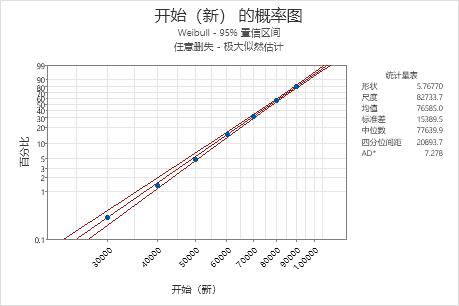
解释
对于新款消声器的数据,点似乎沿着拟合线分布。因此,可以假定对数据选择 Weibull 分布很合适。拟合线基于 Weibull 分布,其中,形状 = 5.76770,尺度 = 82733.7。
生存图
生存图描述物品在特定时间之前能够使用的概率。因此,生存图显示产品在一段时间内的可靠性。
- 中心线是一段时间内的估计可靠性。
- 右侧的线连接每个时间点的可靠性上限。左侧的线连接每个时间点的可靠性下限。
将指针放在生存曲线上时,Minitab 将显示一个包含时间和生存概率的表格。
仅当分布充分拟合数据时,才能使用此图。如果分布对数据的拟合效果很差,则这些估计值将不准确。使用分布 ID 图、概率图和拟合优度度量可确定分布是否充分拟合了数据。
示例输出
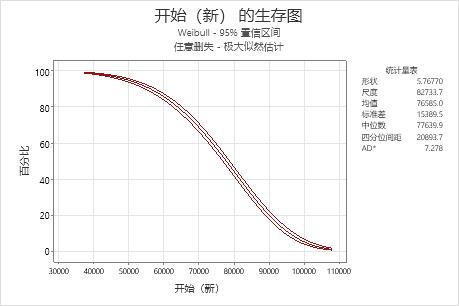
解释
对于新款消声器的数据,新款消声器在 50,000 英里后失效的概率大约为 95%。生存函数基于 Weibull 分布,其中,形状 = 5.76770,尺度 = 82733.7。
累积失效图
为了从产品失效时间的角度描述产品的可靠性,累积失效图显示了在特定时间 t 后失效的项目的累积百分比。累积失效函数表示 1 − 生存函数。
- 中心线是在一段时间内的估计累积失效百分比。
- 右侧的线连接每个时间点的累积失效百分比下限。左侧的线连接每个时间点的累积失效百分比上限。
将指针放在曲线上时,Minitab 显示累积失效概率和失效时间。
仅当分布充分拟合数据时,才能使用此图。如果分布对数据的拟合效果很差,则这些估计值将不准确。使用分布 ID 图、概率图和拟合优度度量可确定分布是否充分拟合了数据。
示例输出
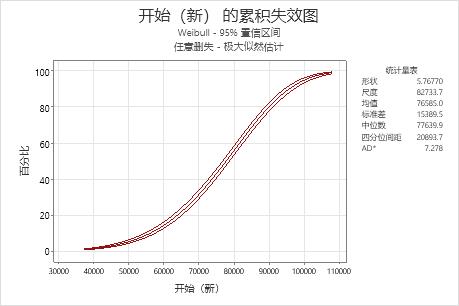
解释
根据新型消声器的数据,新型消声器在 50,000 英里后失效的概率大约为 5%。累积失效函数基于 Weibull 分布,其中,形状 = 5.76770,尺度 = 82733.7。
故障图
- 递减:物品因老化而失效的几率较小。递减故障通常发生在产品寿命的早期阶段。
- 固定:物品以固定速率失效。固定故障通常发生在产品“使用寿命”期内,在这期间内会随机出现失效情况。
- 递增:物品因老化而失效的几率较大。递增故障通常发生在产品寿命的后期阶段,例如发生在磨损期。
故障函数的形状是基于数据和所选分布确定的。将指针放在故障曲线上时,Minitab 将显示一个包含失效时间和瞬时故障率的表格。
仅当分布充分拟合数据时,才能使用此图。如果分布对数据的拟合效果很差,则这些估计值将不准确。使用分布 ID 图、概率图和拟合优度度量可确定分布是否充分拟合了数据。
示例输出
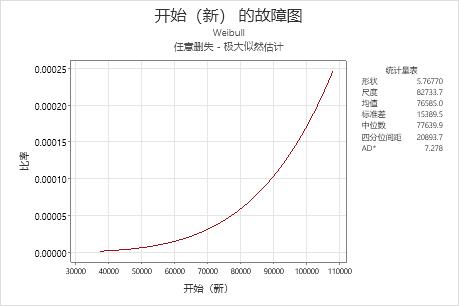
解释
根据新型消声器的数据,故障函数基于 Weibull 分布,其中,形状 = 5.76770,尺度 = 82733.7。在本例中,瞬时故障率随时间而递增,这意味着新型消声器随着老化而更易失效。
多种失效模式图
对于多种失效数据,Minitab 将针对每种失效模式显示相应的图形。
- 使用概率图可评估所选分布对数据的拟合程度。如果这些点位于拟合线附近,则使用该分布可对数据进行建模。
- 使用生存图可评估物品在特定时间之前能够使用的概率。因此,生存图显示产品在一段时间内的可靠性。
- 使用故障函数可将失效似然用作单元持续时间的函数(在特定时间 t 的瞬时失效率)。故障图显示一段时间内的失效率趋势。
示例输出
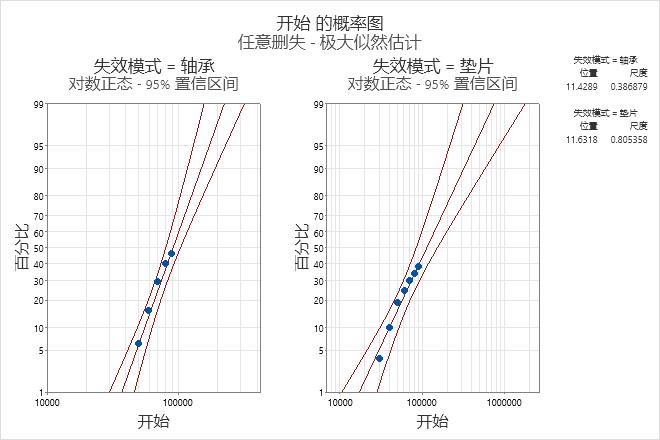
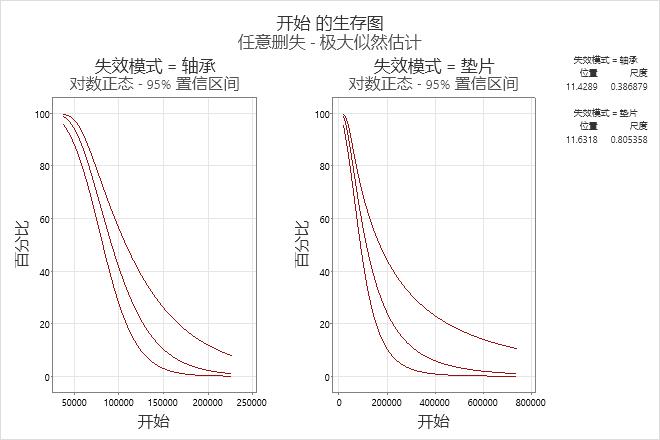
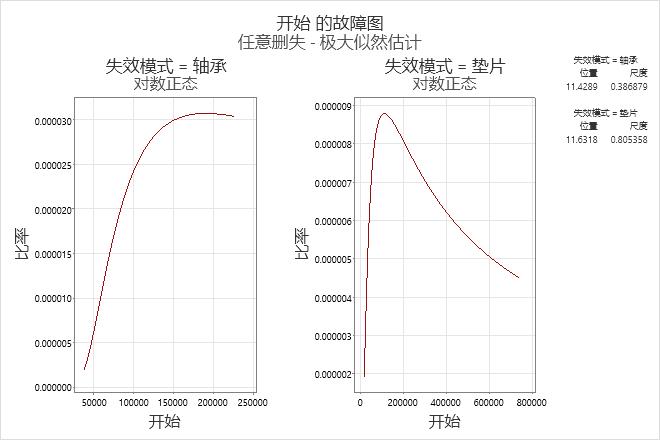
解释
对于水泵数据,对数正态分布似乎是对两种失效模式建模的合适选择。轴承失效的参数为位置 = 11.4289,尺度 = 0.386879,垫圈失效的参数为位置 = 11.6318,尺度 = 0.805358。
水泵在 70,000 英里后没有出现轴承失效的概率是 70%,没有出现垫圈失效的概率是 70%。
每种失效模式的失效率随时间稍有增加,但随后垫圈失效的失效率将降低。
