一位可靠性工程师想评估新型消声器的可靠性,并估计预期 50,000 英里保修的保证索赔的比率。工程师收集了新旧两种类型的消声器的失效数据。每隔 10,000 英里对消声器进行一次失效检测。
工程师记录每个 10,000 英里间隔的失效次数。因此,数据为任意删失。工程师使用参数分布分析(任意删失)来确定如下内容:
- 不同百分比消音器失效的英里数
- 运行将超过 50,000 英里的消音器所占的百分比
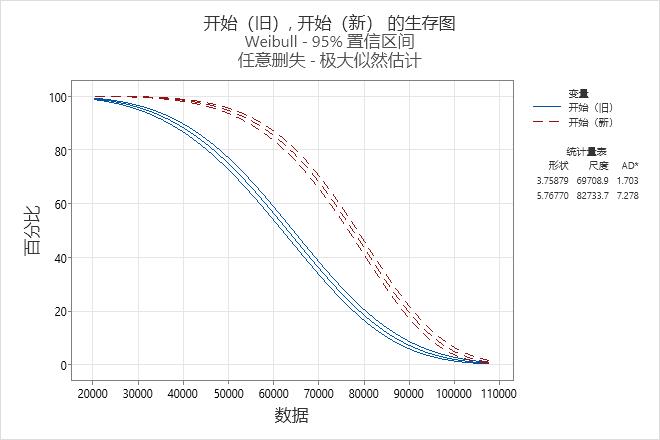
- 消音器的生存函数(如生存图上所示)
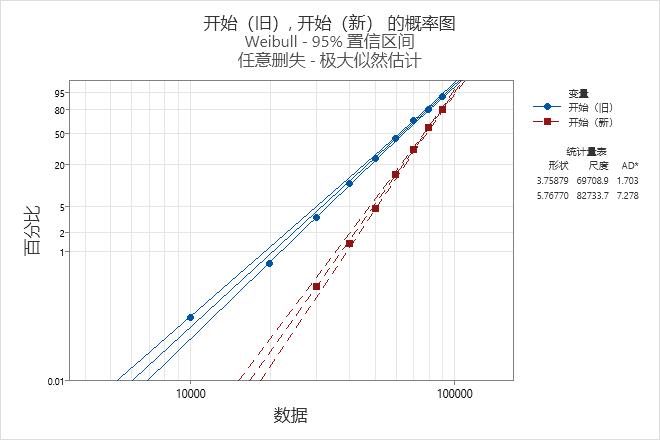
- 数据对 Weibull 分布的拟合程度(如概率图上所示)
- 打开样本数据,消声器可靠性.MWX。
- 选择。
- 在初始变量中,输入开始(旧)开始(新)。
- 在结尾变量中,输入结束(旧)结束(新)。
- 在频率列(可选)中,输入频率(旧)频率(新)。
- 从假定分布中,选择Weibull。
- 单击估计。在估计这些时间(值)的概率中,输入 50000。单击确定。
- 单击图形。选择生存图。
- 在每个对话框中单击确定。
解释结果
工程师可以使用百分位数表确定各种百分比的旧消声器和新消声器失效时已行驶的英里数。对于旧消声器,10% 的消声器在 38,307 英里之前失效。对于新消声器,10% 的消声器在 56,006.1 英里之前失效。
使用生存概率图,工程师可以确定有多大比例的消声器预计将至少在 50,000 英里前可用。对于旧消声器,在 50,000 英里之后生存的概率大约为 75.07%。对于新消声器,在 50,000 英里后生存的概率大约为 94.67%。
工程师使用生存图查看不同英里数下的生存概率,使用概率图检查 Weibull 分布是否能够充分拟合数据。
- 旧消声器
- 变量起始:开始(旧) 结束: 结束(旧)频率: 频率(旧)
删失
删失信息 计数 右删失值 83 区间删失值 965 左删失值 1 估计法:极大似然分布: Weibull参数估计
95.0% 正态置信区间 参数 估计 标准误 下限 上限 形状 3.75879 0.100226 3.56739 3.96045 尺度 69708.9 618.000 68508.1 70930.7 对数似然 = -2083.927拟合优度
Anderson-Darling
(已调整)1.703 分布特征
95.0% 正态置信区间 估计 标准误 下限 上限 均值(MTTF) 62963.8 585.834 61826.0 64122.5 标准差 18685.0 417.812 17883.8 19522.1 中位数 63232.6 618.048 62032.7 64455.6 下四分位数(Q1) 50042.1 692.162 48703.7 51417.3 上四分位数(Q3) 76037.5 658.037 74758.6 77338.2 四分位间距(IQR) 25995.4 610.478 24826.0 27219.9 百分位数表格
95.0% 正态置信区间 百分比 百分位数 标准误 下限 上限 1 20501.3 730.973 19117.5 21985.2 2 24686.2 762.138 23236.7 26226.0 3 27535.4 773.441 26060.5 29093.8 4 29766.4 777.507 28280.8 31329.9 5 31630.7 778.040 30141.9 33193.0 6 33249.1 776.589 31761.3 34806.5 7 34689.8 773.926 33205.6 36240.3 8 35995.3 770.488 34516.4 37537.6 9 37194.3 766.537 35721.9 38727.5 10 38307.0 762.243 36841.8 39830.5 20 46771.7 714.662 45391.8 48193.6 30 52987.5 671.735 51687.1 54320.5 40 58301.0 638.544 57062.8 59566.1 50 63232.6 618.048 62032.7 64455.6 60 68106.3 614.500 66912.5 69321.4 70 73237.9 634.997 72003.8 74493.1 80 79117.5 693.244 77770.3 80487.9 90 87026.8 827.620 85419.8 88664.1 91 88068.9 849.547 86419.5 89749.8 92 89195.0 874.226 87497.9 90925.0 93 90425.9 902.323 88674.6 92211.8 94 91791.7 934.808 89977.7 93642.3 95 93338.0 973.162 91450.0 95265.0 96 95139.2 1019.83 93161.2 97159.2 97 97330.7 1079.31 95238.2 99469.3 98 100206 1161.47 97954.9 102508 99 104650 1296.79 102139 107223 生存概率表
95.0% 正态置信区间 时间摘录 (Time) 概率 下限 上限 50000 0.750682 0.727911 0.771856 - 新消声器
- 变量起始:开始(新) 结束: 结束(新)频率: 频率(新)
删失
删失信息 计数 右删失值 210 区间删失值 839 估计法:极大似然分布: Weibull参数估计
95.0% 正态置信区间 参数 估计 标准误 下限 上限 形状 5.76770 0.174361 5.43589 6.11977 尺度 82733.7 501.285 81757.0 83722.0 对数似然 = -1804.510拟合优度
Anderson-Darling
(已调整)7.278 分布特征
95.0% 正态置信区间 估计 标准误 下限 上限 均值(MTTF) 76585.0 488.710 75633.1 77548.8 标准差 15389.5 407.421 14611.4 16209.1 中位数 77639.9 501.312 76663.5 78628.7 下四分位数(Q1) 66660.6 610.001 65475.7 67866.9 上四分位数(Q3) 87554.2 543.215 86496.0 88625.4 四分位间距(IQR) 20893.7 591.844 19765.3 22086.5 百分位数表格
95.0% 正态置信区间 百分比 百分位数 标准误 下限 上限 1 37265.1 938.485 35470.3 39150.6 2 42060.6 910.590 40313.2 43883.7 3 45163.8 884.871 43462.4 46931.9 4 47516.0 861.886 45856.4 49235.7 5 49434.9 841.147 47813.5 51111.3 6 51068.9 822.219 49482.6 52706.1 7 52500.3 804.776 50946.5 54101.6 8 53779.7 788.572 52256.1 55347.7 9 54940.5 773.424 53445.3 56477.5 10 56006.1 759.186 54537.7 57514.0 20 63788.2 649.873 62527.1 65074.7 30 69192.0 576.979 68070.3 70332.1 40 73638.2 528.302 72609.9 74680.9 50 77639.9 501.312 76663.5 78628.7 60 81489.1 497.212 80520.4 82469.5 70 85439.7 519.747 84427.0 86464.5 80 89849.4 577.132 88725.4 90987.7 90 95605.5 695.279 94252.5 96978.0 91 96350.1 713.480 94961.8 97758.6 92 97151.1 733.704 95723.7 98599.9 93 98022.8 756.429 96551.4 99516.6 94 98985.2 782.340 97463.6 100530 95 100069 812.488 98488.8 101674 96 101323 848.595 99673.3 103000 97 102838 893.813 101101 104605 98 104808 955.006 102952 106696 99 107814 1053.11 105770 109898 生存概率表
95.0% 正态置信区间 时间摘录 (Time) 概率 下限 上限 50000 0.946704 0.935996 0.955664