Kaplan-Meier 估计
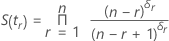
其中,S(t0) = 1,t0 = 0。
经验故障函数
故障函数描述某个区间的失效率。在第一个删失观测值之前,故障函数为 0。故障函数仅在非删失的观测值处进行更改。在最后一个非删失数据点之后,Minitab 不绘制故障函数。

当存在约束时,Minitab 使用约束中的最大排秩来估计故障函数。有关更多详细信息,请参见 Nelson1。
平均失效时间
对于非删失数据,失效时间均值与平均失效时间相等。下面是与删失数据或非删失数据一起使用的常见公式:
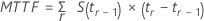
而且,当最大观测值为删失观测值时,Minitab 将最大的非删失观测值视为时间限值来进行计算。有关更多详细信息,请参见 Lee2。
MTTF 的标准误
失效时间均值的标准误是方差的平方根。当所有的观测值都是非删失观测值时,Minitab 计算无偏估计值:
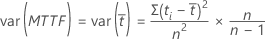
对于某些数据是删失数据的情况,方差的无偏估计值采用如下公式:

由于经验故障函数的形状,生存曲线下方的面积 Ar 是矩形面积,矩形的高度等于生存函数,长度等于非删失观测值之间的间隔。
表示法
| 项 | 说明 |
|---|---|
| tr | 具有排秩 r 的数据点的时间 |
| r | 数据点的排秩,最早的失效具有最低的排秩 |
| n | 单位总数 |
| δr | 0(如果第 j 个观测值是删失的)或 1(如果第 j 个观测值是非删失的) |
| c | 直到下个非删失观测值之前的数据点数 |
| S(tr) | 时间 tr 处的经验生存函数 |
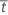 | 平均失效应力 |
| Ar | tr 右侧生存图曲线下方的面积 |
| m | 非删失观测值总数 |
参考资料
1. W. Nelson (1982)。Applied Life Data Analysis(应用寿命数据分析)。John Wiley & Sons, Inc. 第 133 页。
2. Elisa T. Lee (1992)。Statistical Methods for Survival Data Analysis(生存数据分析的统计方法),第 2 版。John Wiley & Sons, Inc. 第 73-76 页。
精算估计
精算模型是一种备择非参数分析,可显示失效时间的分组信息。Kaplan-Meier 方法假设在出现失效之后,某个区间中的延期出现在该区间的末尾。Minitab 的精算模型假设延期出现在该区间的中间,这会导致区间中的可用单元数减少。使用估计法的生存函数的估计值如下所示:
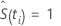 对于 i = 0
对于 i = 0
 对于 i > 0
对于 i > 0
经验故障函数
故障函数描述某个区间的失效率。使用精算估计,假设计算针对的是区间的中点。在故障图上,函数是从中点到中点绘制的。有关更多详细信息,请参见“表示法”部分后面的参考资料。
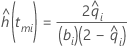
表示法
| 项 | 说明 |
|---|---|
| ni | 进入某个区间的单元的数量 |
| di | 在该区间中失效的编号 |
| n'i |  |
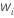 | 某个区间中删失的编号 |
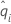 | 事件的条件概率,等于 di/n'i |
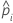 |  |
| tmi | 位于精算区间中点的时间 |
| bi | 精算区间的长度 |
参考资料
Collett, D. (1994)。Modelling Survival Data in Medical Research(对医药研究中的生存数据建模),Chapman and Hall。
Lee, Elisa T. (1992)。Statistical Methods for Survival Data Analysis(生存数据分析的统计方法),第 2 版,John Wiley & Sons。
Turnbull 估计
Turnbull1, 2 开发了一种为数据的累积分布函数计算非参数最大似然估计值的迭代算法。此方法适用于更常见的情形,例如,在区间出现重叠时。
Minitab 显示的输出中汇总了区间概率的 Turnbull 估计值,以及这些概率的标准误。
参考资料
- B.W. Turnbull (1976)。“The Empirical Distribution Function with Arbitrarily Grouped, Censored and Truncated Data”(具有任意分组、删失和截尾数据的经验分布函数),Journal of the Royal Statistical Society(皇家统计学会杂志),第 38 期,第 290-295 页。
- B.W. Turnbull (1974)。“Nonparametric Estimation of a Survivorship Function with Doubly Censored Data”(具有双删失数据的生存函数的非参数估计),Journal of the American Statistical Association(美国统计协会杂志),第 69 卷,第 345 期,第 169-173 页。
置信区间
无论采用哪种估计法,Minitab 都使用正态近似来计算置信区间。置信区间如下所示:
公式
生存概率的估计值  zα × 估计值的标准误
zα × 估计值的标准误
表示法
| 项 | 说明 |
|---|---|
| zα | 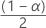 标准正态分布的临界值上限 标准正态分布的临界值上限 |
| α | 置信水平 |
