渐近方差
AVar (MLE) 是渐近方差,ACov (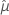 ,
, ) 是 μ、σ、θ 和 β(从 Fisher 信息矩阵的逆矩阵的相应元素提取)的 MLE 的渐近协方差。有关更多信息,请参见 Meeker 和 Escobar1。
) 是 μ、σ、θ 和 β(从 Fisher 信息矩阵的逆矩阵的相应元素提取)的 MLE 的渐近协方差。有关更多信息,请参见 Meeker 和 Escobar1。
百分位数案例
估计百分位数 tp 所需的样本数量的计算公式如下:
对数、Logistic 和最小极值分布
- 对于双侧置信区间

- 对于单侧置信区间


| 项 | 说明 |
|---|---|
| N | 样本数量 |
| tp,mle | tp 的 ML 估计值 |
| DT | 估计值和 (1 – α)100% 置信区间的上限(或下限)之间的距离 |
| Φ-1 | 所选模型的逆 CDF |
| Φ-1 nor | 正态分布的逆 CDF |
Weibull、对数正态和对数 Logistic 模型
- 对于双侧置信区间

- 对于单侧置信区间


| 项 | 说明 |
|---|---|
| N | 样本数量 |
| tp,mle | tp 的 ML 估计值 |
| RT | 当 (1 – α)100% 置信区间的上限(或下限)与 MLE 的距离为 X% 时的精确度。对于上限,RT =1 + X/100。对于下限,RT = 1/(1-X/100)。 |
| Φ-1 | 所选模型的逆 CDF |
| Φ-1 nor | 正态分布的逆 CDF |
可靠性案例
- 对于双侧置信区间
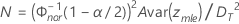
- 对于单侧置信区间
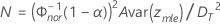
其中,


 对于下限
对于下限
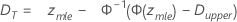 对于上限
对于上限
 对于正态、Logistic 和最小极值分布
对于正态、Logistic 和最小极值分布
 对于 Weibull、对数正态和对数 Logistic 分布
对于 Weibull、对数正态和对数 Logistic 分布
| 项 | 说明 |
|---|---|
| N | 样本数量 |
| μmle | 均值(正态和 Logistic)、位置(最小极值)或对数-位置(对数正态和对数 Logistic)的 MLE 估计值 |
| σmle | 尺度参数的 MLE 估计值 |
| DT | 精确度 |
| Φ-1 | 所选模型的逆 CDF |
| Φ-1 nor | 正态分布的逆 CDF |
1 W.Q. Meeker 和 L.A. Escobar (1998)。Statistical Methods for Reliability Data(可靠性数据的统计方法)。John Wiley & Sons, Inc.
