参数估计值
公式
| 分布 | 参数 |
|---|---|
|
最小极值 正态 Logistic |
μ = 位置， σ = 尺度，σ > 0 |
|
对数正态 对数 Logistic |
μ = 位置，μ > 0 σ = 尺度， σ > 0 |
|
3 参数对数正态 3 参数对数 Logistic |
μ = 位置，μ > 0 σ = 尺度，σ > 0 λ = 阈值。 |
|
Weibull |
α = 尺度，α = exp(μ) β = 形状，β = 1/σ |
|
3 参数 Weibull |
α = 尺度，α = exp(μ) β = 形状，β = 1/σ λ = 阈值， |
|
指数 |
θ = 尺度，θ > 0 |
|
双参数指数 |
θ = 尺度，θ > 0 λ = 阈值， |
参数估计值的标准误
标准误是参数估计值的标准差。标准误提供每个估计值中变异性的度量。
, 
, 
, 
, 
，和 
表示 μ、σ、α、β、θ 和 λ 的 MLE 的标准误。每个标准误等于 Fisher 信息矩阵的逆矩阵的相应对角线单元的平方根。
参数估计值的置信限
公式
| 分布 | 参数 | 置信下限 | 置信上限 |
|---|---|---|---|
| 最小极值、正态、Logistic、对数正态和对数 Logistic | 位置 μ |
 |
 |
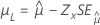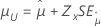| 尺度 σ |
 |
 |
|
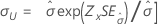| 3 参数对数正态、3 参数对数 Logistic | 位置 μ |
 |
 |
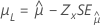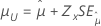| 尺度 σ |
 |
 |
|
| 阈值 λ |
 |
 |
|
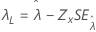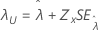| Weibull | 形状 β |
 |
 |
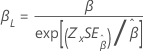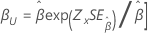| 尺度 α |
 |
 |
|
|
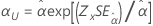3 参数 Weibull |
形状 β |
 |
 |
|
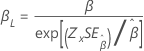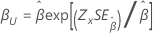尺度 α |
 |
 |
|
|
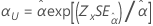阈值 λ |
 |
 |
|
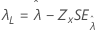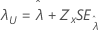| 指数 | 尺度 |
 |
 |
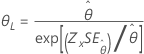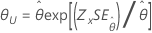| 双参数指数 | 尺度 θ |
 |
 |
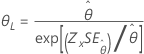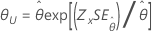| 阈值 λ |
 |
 |
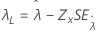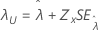注意
对于某些数据，似然函数无边界，因此，会为具有一个阈值参数的分布（如双参数指数分布）生成不一致的估计值。如果发生这种情况，将无法以数值方式确定估计参数的方差-协方差矩阵。在这种情况下，Minitab 假定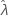 
是固定的，并导致 SE (
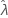) = 0。
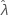的上限和下限为 
。
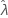表示法
| 项 | 说明 |
|---|---|
| zx | 标准正态分布的 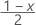 临界值上限，在该分布中，100x % 是置信水平，0 < x < 1。 |
