某可靠性工程师想研究涡轮装置中发动机绕组的失效率以确定绕组失效的时间。在高温下,绕组可能会分解过快。
该工程师记录发动机绕组在 80° C 和 100° C 下的失效时间。但是,对于某些部件,必须在其失效之前将其从检验中去除。因此,数据为右删失数据。该工程师使用分布概要图(右删失)来将对数正态分布与数据拟合并直观地评估生产率和失效率与时间的关系。
- 打开样本数据,发动机绕组可靠性.MWX。
- 选择。
- 在变量中,输入80 度100 度。
- 选择参数分析。从分布中,选择对数正态。
- 单击删失。在使用删失列下,输入80 度删失100 度删失。
- 在删失值中,键入 0。
- 在每个对话框中单击确定。
解释结果
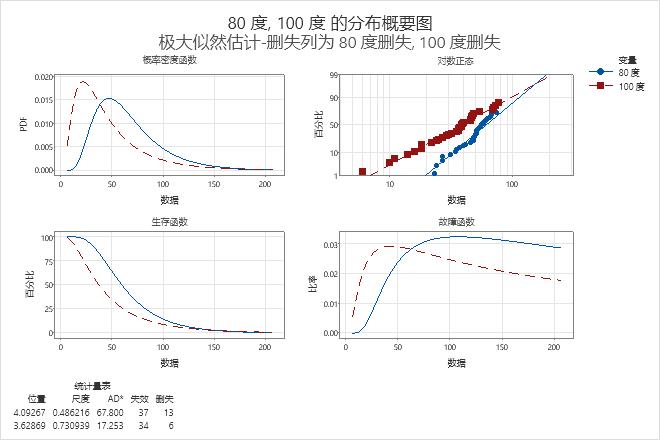
概率图显示这两个变量的失效时间点大致位于直线上。因此,这两个变量的对数正态分布能够很好地拟合数据。
使用故障函数图可以比较不同变量的失效率。例如,在 100° C 时,失效率最初大于 80° C 的失效率,在大约 40 小时处达到峰值(大约为 0.03)。在 80° C 时,失效率增加得更慢,在大约 50 小时处达到峰值(大约为 0.032 以上)。
使用生存函数图可以比较不同变量的生存率。例如,在小于大约 150 小时的时间处,在 80° C 下生存的绕组所占的百分比比 100° C 下大得多。在 150 小时后,这两个温度下生存的绕组所占的百分比变得几乎相等。