关于本主题
百分位数和百分位数的标准误
百分位数用来估计总体的一定百分比发生失效的时间。默认情况下,Minitab 显示百分位数表格,以供对常见的百分位数进行参数分布分析。
百分位数的标准误是方差的平方根。
 ,
,  ,
,  ,
,  ,
,  ,
, 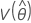 ,
, 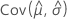 ,
, 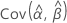 ,
, 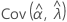 ,
, 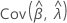 ,
, 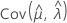 和
和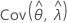 表示 μ、σ、α、β、θ 和 λ(从 Fisher 信息矩阵的逆矩阵的相应单元提取)的 MLE 的方差和协方差。
表示 μ、σ、α、β、θ 和 λ(从 Fisher 信息矩阵的逆矩阵的相应单元提取)的 MLE 的方差和协方差。
用于每个分布的百分位数和方差估计值的公式如下所示:
最小极值
- 百分位数
-
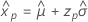
- 单方差
-
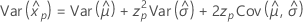
Weibull
- 百分位数
-

- 单方差
-
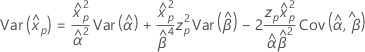
3 参数 Weibull
- 百分位数
-

- 单方差
-
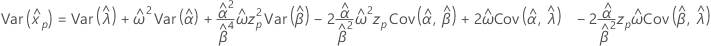
指数
- 百分位数
-

- 单方差
-

双参数指数
- 百分位数
-

- 单方差
-
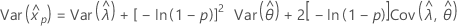
正常
- 百分位数
-
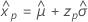
- 单方差
-
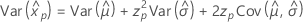
对数正态
- 百分位数
-

- 单方差
-
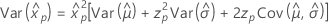
3 参数对数正态
- 百分位数
-

- 单方差
-
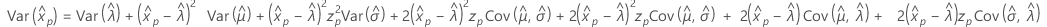
Logistic
- 百分位数
-
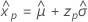
- 单方差
-
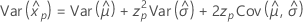
对数 Logistic
- 百分位数
-
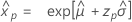
- 单方差
-
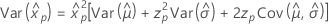
3 参数对数 Logistic
- 百分位数
-

- 单方差
-

表示法
| 项 | 说明 |
|---|---|
| zp |
标准分布的、在 p(标准分布的第 p 个百分位数)处求值的逆 CDF |
百分位数的置信限
| 分布 | 置信限 |
|---|---|
|
最小极值 正态 Logistic |
  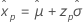 |
|
Weibull 指数 对数正态 对数 Logistic |
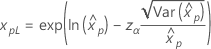 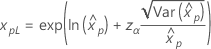 其中, |
|
3 参数 Weibull 双参数指数 3 参数对数正态 3 参数对数 Logistic |
如果 λ < 0:   如果 λ 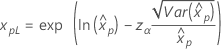 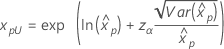 其中, |
如果要为估计的 xp 计算方差,请参见“百分位数和百分位数的标准误”。
表示法
| 项 | 说明 |
|---|---|
| zα | 标准正态分布的 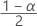 临界值上限,在该分布中,100α % 是置信水平。 临界值上限,在该分布中,100α % 是置信水平。 |