某可靠性工程师想研究涡轮装置中发动机绕组的失效率以确定绕组失效的时间。在高温下,绕组可能会分解过快。
该工程师记录发动机绕组在各个温度下的失效时间。但是,对于某些部件,必须在其失效之前将其从检验中去除。因此,数据为右删失数据。该工程师使用分布 ID 图(右删失)为在 80° C 下收集的数据选择分布模型。
- 打开样本数据,发动机绕组可靠性.MWX。
- 选择。
- 在变量中,输入80 度。
- 选择指定。确保选中了默认分布(Weibull、对数正态、指数和正态)。
- 单击删失。在使用删失列下面,输入80 度删失。
- 在删失值中,键入 0。
- 在每个对话框中单击确定。
解释结果
失效时间点大致落在对数正态概率图上的直线上。因此,对数正态分布提供很好的拟合。工程师于是决定使用对数正态分布来对 80° C 下收集的数据进行建模。
Minitab 还显示一个百分位数表和一个平均故障时间间隔 (MTTF) 表,这两个表提供针对每个分布计算的失效时间。您可以通过比较计算的值来查看您的结论如何随不同的分布变化。如果多个分布能够很好地拟合数据,您可能希望使用提供最保守结果的分布。
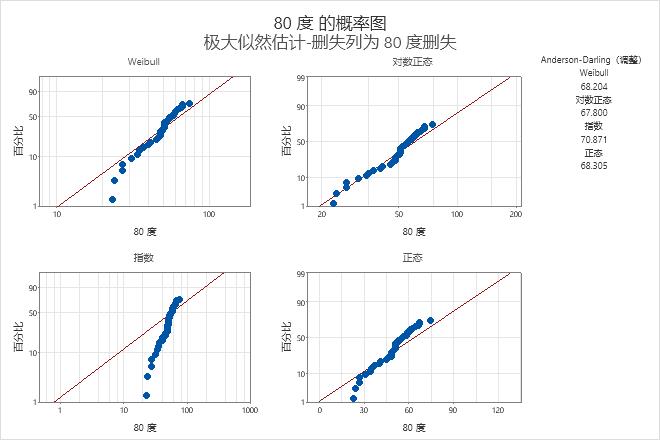
拟合优度
| 分布 | Anderson-Darling (调整) |
|---|---|
| Weibull | 68.204 |
| 对数正态 | 67.800 |
| 指数 | 70.871 |
| 正态 | 68.305 |
百分位数表格
| 95% 正态置信区间 | |||||
|---|---|---|---|---|---|
| 分布 | 百分比 | 百分位数 | 标准误 | 下限 | 上限 |
| Weibull | 1 | 10.0765 | 2.78453 | 5.86263 | 17.3193 |
| 对数正态 | 1 | 19.3281 | 2.83750 | 14.4953 | 25.7722 |
| 指数 | 1 | 0.809731 | 0.133119 | 0.586684 | 1.11758 |
| 正态 | 1 | -0.549323 | 8.37183 | -16.9578 | 15.8592 |
| Weibull | 5 | 20.3592 | 3.79130 | 14.1335 | 29.3273 |
| 对数正态 | 5 | 26.9212 | 3.02621 | 21.5978 | 33.5566 |
| 指数 | 5 | 4.13258 | 0.679391 | 2.99422 | 5.70371 |
| 正态 | 5 | 18.2289 | 6.40367 | 5.67790 | 30.7798 |
| Weibull | 10 | 27.7750 | 4.11994 | 20.7680 | 37.1463 |
| 对数正态 | 10 | 32.1225 | 3.09409 | 26.5962 | 38.7970 |
| 指数 | 10 | 8.48864 | 1.39552 | 6.15037 | 11.7159 |
| 正态 | 10 | 28.2394 | 5.48103 | 17.4968 | 38.9820 |
| Weibull | 50 | 62.6158 | 4.62515 | 54.1763 | 72.3700 |
| 对数正态 | 50 | 59.8995 | 4.31085 | 52.0192 | 68.9735 |
| 指数 | 50 | 55.8452 | 9.18089 | 40.4622 | 77.0766 |
| 正态 | 50 | 63.5518 | 4.06944 | 55.5759 | 71.5278 |
平均故障时间间隔表格
| 95% 正态置信区间 | ||||
|---|---|---|---|---|
| 分布 | 均值 | 标准误 | 下限 | 上限 |
| Weibull | 64.9829 | 4.6102 | 56.5472 | 74.677 |
| 对数正态 | 67.4153 | 5.5525 | 57.3656 | 79.225 |
| 指数 | 80.5676 | 13.2452 | 58.3746 | 111.198 |
| 正态 | 63.5518 | 4.0694 | 55.5759 | 71.528 |
