一位可靠性工程师想评估新型消声器的可靠性,并估计预期 50,000 英里保修的保证索赔的比率。工程师收集了新旧两种类型的消声器的失效数据。每隔 10,000 英里对消声器进行一次失效检测。
工程师记录每个 10,000 英里间隔的失效次数。因此,数据为任意删失。在使用参数分布分析(任意删失)分析新消音器的失效数据之前,工程师使用分布 ID 图(任意删失)选择要分析的分布模型。
- 打开样本数据,消声器可靠性.MWX。
- 选择。
- 在初始变量中,输入开始(新)。
- 在结尾变量中,输入结束(新)。
- 在频率列(可选)中,输入频率(新)。
- 选择指定。确保选中了默认分布(Weibull、对数正态、指数和正态)。
- 单击确定。
解释结果
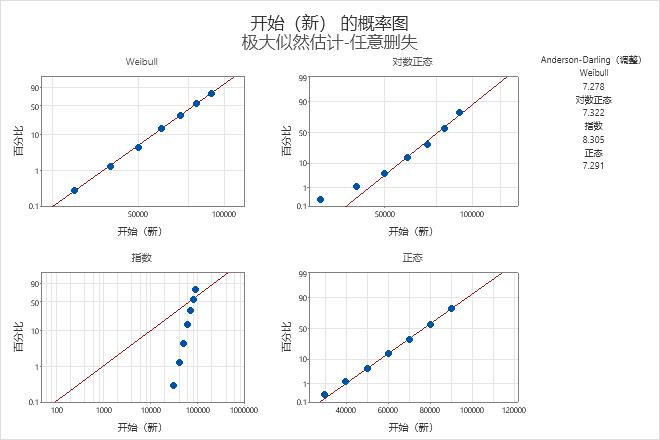
在 Weibull 概率图上,点大致落在直线上。因此,Weibull 分布提供很好的拟合。工程师决定使用 Weibull 分布对参数分布分析(任意删失)的数据建模。
Minitab 还显示一个百分位数表和一个平均故障时间间隔 (MTTF) 表,这两个表提供针对每个分布计算的失效时间。您可以通过比较计算的值来查看您的结论如何随不同的分布变化。如果多个分布能够很好地拟合数据,您可能希望使用提供最保守结果的分布。
使用 频率(新) 中的频率
拟合优度
| 分布 | Anderson-Darling (调整) |
|---|---|
| Weibull | 7.278 |
| 对数正态 | 7.322 |
| 指数 | 8.305 |
| 正态 | 7.291 |
百分位数表格
| 95% 正态置信区间 | |||||
|---|---|---|---|---|---|
| 分布 | 百分比 | 百分位数 | 标准误 | 下限 | 上限 |
| Weibull | 1 | 37265.1 | 938.485 | 35470.3 | 39150.6 |
| 对数正态 | 1 | 43817.7 | 688.033 | 42489.7 | 45187.2 |
| 指数 | 1 | 941.789 | 32.5296 | 880.143 | 1007.75 |
| 正态 | 1 | 39810.3 | 1047.34 | 37757.6 | 41863.1 |
| Weibull | 5 | 49434.9 | 841.147 | 47813.5 | 51111.3 |
| 对数正态 | 5 | 51458.9 | 624.451 | 50249.5 | 52697.5 |
| 指数 | 5 | 4806.55 | 166.019 | 4491.93 | 5143.21 |
| 正态 | 5 | 50694.9 | 810.524 | 49106.3 | 52283.5 |
| Weibull | 10 | 56006.1 | 759.186 | 54537.7 | 57514.0 |
| 对数正态 | 10 | 56063.1 | 585.905 | 54926.4 | 57223.3 |
| 指数 | 10 | 9873.05 | 341.017 | 9226.79 | 10564.6 |
| 正态 | 10 | 56497.5 | 699.183 | 55127.1 | 57867.8 |
| Weibull | 50 | 77639.9 | 501.312 | 76663.5 | 78628.7 |
| 对数正态 | 50 | 75850.3 | 576.625 | 74728.5 | 76988.9 |
| 指数 | 50 | 64952.9 | 2243.49 | 60701.3 | 69502.3 |
| 正态 | 50 | 76966.0 | 514.756 | 75957.1 | 77974.9 |
平均故障时间间隔表格
| 95% 正态置信区间 | ||||
|---|---|---|---|---|
| 分布 | 均值 | 标准误 | 下限 | 上限 |
| Weibull | 76585.0 | 488.71 | 75633.1 | 77549 |
| 对数正态 | 77989.9 | 615.96 | 76792.0 | 79207 |
| 指数 | 93707.3 | 3236.67 | 87573.5 | 100271 |
| 正态 | 76966.0 | 514.76 | 75957.1 | 77975 |
