检验时间
在置信水平 100(1 – α)% 下,按如下方式计算为了证实重新设计的系统已显著改善而检验的最小分量数 N 时,每个系统的检验时间:
- 当 m = 0 时(0 失效检验计划)

- 当 m > 0 时(m 失效检验计划)
对 R 的方程求解(请参见验证检验计划中 M 失效检验计划的方法和公式中的“方程”部分)。然后获得如下形式的 t:

表示法
| 项 | 说明 |
|---|---|
| t | 时间 |
| m | 失效数 |
| α | 显著性水平 (alpha),等于 1 – 置信水平 |
| N | 要检验的最小分量数 |
| R0 | 限制在区间 (0,1) 中的解 |
| R–1(t) | 逆可靠性函数 |
样本数量
在置信水平 100(1 – α)% 下,按如下方式计算为了证实重新设计的系统已显著改善而检验的最小系统数量:
- 当 m = 0 时(0 失效检验计划)
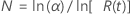
- 当 m > 0 时(m 失效检验计划)
对 N 的方程求解(请参见验证检验计划中 M 失效检验计划的方法和公式中的“方程”部分)。使用以下值作为起始值:
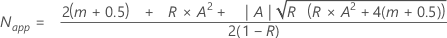
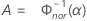
表示法
| 项 | 说明 |
|---|---|
| t | 时间 |
| m | 失效数 |
| α | 显著性水平 (alpha),等于 1 – 置信水平 |
| N | 要检验的最小系统数 |
| R(t) | 可靠性函数 |
| R–1(t) | 逆可靠性函数 |
