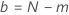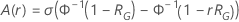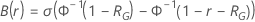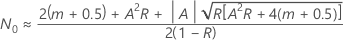通过测试计划的概率的计算取决于对失败进行模型的分布。对于日志位置比例分布,概率是改进比率的函数。对于位置比例分布,概率是改进量的函数。公式的表达式整齐地分为两个情况,这取决于您是指定样本大小还是测试时间。
样本数量
当演示测试的规范包括样本大小时,通过概率的计算需要测试时间。对于给定的样本大小, 置信度满足以下等式:
置信度满足以下等式:
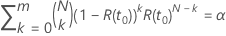
 置信度满足以下等式:
置信度满足以下等式:
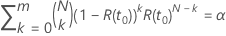
在时间点上  ,解决方案,
,解决方案,
 的方程有以下形式:
的方程有以下形式:
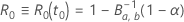
 ,解决方案,
,解决方案,
 的方程有以下形式:
的方程有以下形式:
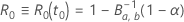
其中,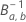 是具有以下形状参数的 beta 分布的反向累积分布函数:
是具有以下形状参数的 beta 分布的反向累积分布函数:
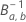 是具有以下形状参数的 beta 分布的反向累积分布函数:
是具有以下形状参数的 beta 分布的反向累积分布函数:
计算  ,反转函数
,反转函数
 。
反转取决于分布系列。
。
反转取决于分布系列。
 ,反转函数
,反转函数
 。
反转取决于分布系列。
。
反转取决于分布系列。
- 日志位置缩放系列

- 位置规模系列
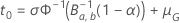
通过测试的概率具有以下形式,取决于  和改进:
和改进: 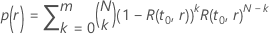
 和改进:
和改进: 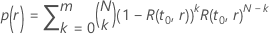
其中,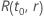 是分布模型的可靠性函数
是分布模型的可靠性函数  and
and 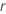 。
。
可靠性功能取决于分布系列:
- 日志位置缩放系列

- 位置规模系列
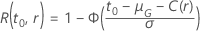
下表提供了  用于分发系列和测试目标:
用于分发系列和测试目标:
| 可靠性目标 | ||||
|---|---|---|---|---|
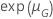
|

|
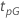
|

|
|
| 日志位置缩放 |  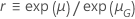 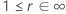 |
 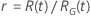  |
 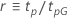 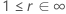 |
  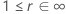 |
| 可靠性目标 | ||||
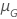
|

|
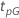
|

|
|
| 位置规模 | 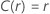  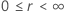 |
 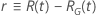  |
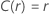  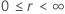 |
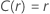 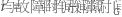 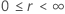 |
在哪里
示例 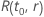 韦布尔分布
韦布尔分布
对于 Weibull 分布的测试计划,可靠性目标为 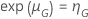 ,和给定的样本大小,通过的概率具有以下形式:
,和给定的样本大小,通过的概率具有以下形式:
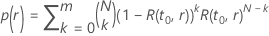
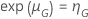 ,和给定的样本大小,通过的概率具有以下形式:
,和给定的样本大小,通过的概率具有以下形式:
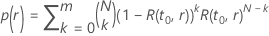
其中,

检验时间
当演示测试的规范包括测试时间时,通过概率的计算需要样本大小。对于给定的测试时间,样本大小为 置信度满足以下等式:
置信度满足以下等式:

 置信度满足以下等式:
置信度满足以下等式:

对于 0 故障测试计划 ( ),方程的解,
),方程的解,
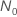 ,
具有以下形式:
,
具有以下形式:
 ),方程的解,
),方程的解,
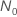 ,
具有以下形式:
,
具有以下形式:
其中,

Minitab 在数字上找到确切的解决方案,当  。
。
通过测试的概率具有以下形式,取决于 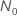 和改进:
和改进: 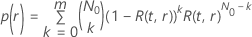
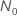 和改进:
和改进: 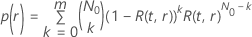
其中,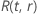 是分布模型的可靠性函数
是分布模型的可靠性函数  和
和
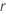 。
。
可靠性功能取决于分布系列 :
- 日志位置缩放系列

- 位置规模系列
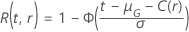
功能  具有与测试规范给出样本大小时相同的定义。
具有与测试规范给出样本大小时相同的定义。
示例 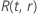 韦布尔分布
韦布尔分布
对于 Weibull 分布的测试计划,可靠性目标为 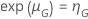 ,在给定的测试时间中,通过的概率具有以下形式:
,在给定的测试时间中,通过的概率具有以下形式:
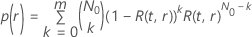
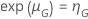 ,在给定的测试时间中,通过的概率具有以下形式:
,在给定的测试时间中,通过的概率具有以下形式:
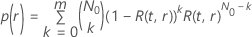
其中,

表示法
| 项 | 说明 |
|---|---|
| N | 当测试的规格提供样本大小时,设计样本大小 |
| m | 检验期间失效的单位数 |
 | 显著性级别,使演示测试的置信度为  |
 | 尺度参数 |
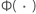 | 所选日志位置缩放或位置缩放的标准分布的累积分布功能 |
 | 所选日志位置缩放或位置缩放的标准分布的反向累积分布函数 |
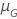 | 满足测试目标的分布的位置参数 |
 | Weibull 分布的形状参数 |
 | 当测试的规格提供样本大小时的测试时间 |
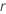 | 日志位置缩放分布的改进比率或位置比例分布的改进量 |
 | 可靠性 t 这是测试的目标 |
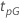 | 百分位数( 百 分比 p,这是测试的目标) |
 | 平均故障时间,这是测试的目标 |
 | 当测试规范提供测试时间时的测试时间 |
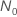 | 当测试规范提供测试时间时,样本大小 |
1 年)W.Q.米克和L.A.埃斯科瓦尔(1998年)。
Statistical Methods for Reliability Data. 威利,纽约