步骤 1:确定模型与数据的拟合优度
- P 值 ≤ α:模型应当充分拟合数据
- 如果 P 值小于或等于显著性水平,则可以断定模型之间在统计上存在显著差异。您应该检查其中任何术语是否具有统计学意义,并确保该模型满足比例危险假设。
- P 值 > α:证据不足,无法得出效应在统计意义上显著的结论。
- 如果 P 值大于显著性水平,则无法得出模型解释响应中变异的结论。您可能希望重新拟合没有该项的模型。
拟合优度检验
| 检验 | 自由度 | 卡方 | P 值 |
|---|---|---|---|
| 似然比 | 4 | 18.31 | 0.001 |
| Wald | 4 | 21.15 | 0.000 |
| 分值 | 4 | 24.78 | 0.000 |
关键结果:P 值
在这些结果中,所有 3 个测试的 p 值都低于 0.05,因此您可以得出结论,该模型非常适合数据。
步骤 2:确定响应和项之间的关联在统计意义上是否显著
- P 值 ≤ α:关联在统计意义上显著
- 如果 P 值小于或等于显著性水平,则可以得出响应变量与项之间的关联在统计意义上显著的结论。
- P 值 > α:关联在统计意义上不显著
- 如果 p 值大于显著性水平,则无法得出响应变量与该项之间的关联在统计意义上显著的结论。您可能希望重新拟合没有该项的模型。
- 如果一个随机因子显著,则可以得出该因子对响应中的变异量有贡献。
- 如果一个协变量在统计意义上显著,则可以得出结论:该协变量的值的变化与平均响应值的变化相关联。
- 如果一个交互作用项的系数显著,则因子与响应之间的关系取决于该项中的其他因子。在这种情况下,不应在不考虑交互作用效应时解释主效应。
- 如果一个多项式项显著,则可以得出数据包含弯曲的结论。
方差分析
| Wald 检验 | |||
|---|---|---|---|
| 来源 | 自由度 | 卡方 | P 值 |
| 年龄 | 1 | 1.78 | 0.182 |
| 舞台 | 3 | 17.92 | 0.000 |
关键结果:P 值
在这些结果中,阶段的 p 值在 0.05 的 α 水平上显着。因此,你可以得出结论,癌症的阶段对患者的生存有统计学上显著的影响。但是,年龄的 p 值为 0.182,因此年龄的影响在 0.05 α水平上并不显著。
步骤 3:确定预测器的相对风险
- 类别变量
-
在分类预测器表的相对风险中,Minitab 将分类变量的两个级别标记为 A 级和 B 级。相对风险描述 A 级相对于 B 级的事件发生率。例如,在以下结果中,第四阶段患者经历该事件的风险比第一阶段患者的风险高 5.5 倍。
- 连续变量
- 在连续预测器的相对风险表中,Minitab 显示变化的单位和相对风险。相对风险描述预测值中每个单位变化的危险率变化。例如,在以下结果中,患者在年龄每增加 1 年时体验该事件的可能性是患者的 1.02 倍。
您可以使用置信区间来确定相对风险是否具有统计学意义。通常,如果置信区间包含 1,则不能断定相对风险具有统计学意义。
连续预测变量的相对风险
| 变更单位 | 相对风险 | 95% 置信区间 | |
|---|---|---|---|
| 年龄 | 1 | 1.0192 | (0.9911, 1.0481) |
类别预测变量的相对风险
| 水平 A | 水平 B | 相对风险 | 95% 置信区间 |
|---|---|---|---|
| 舞台 | |||
| II | I | 1.1503 | (0.4647, 2.8477) |
| III | I | 1.9010 | (0.9459, 3.8204) |
| IV | I | 5.5068 | (2.4086, 12.5901) |
| III | II | 1.6526 | (0.6819, 4.0049) |
| IV | II | 4.7872 | (1.7825, 12.8566) |
| IV | III | 2.8968 | (1.2952, 6.4788) |
关键结果:相对风险,95% CI
步骤 4:确定模型是否满足比例危险假设
- 比例危险表测试
-
使用测试来确定模型是否符合比例危险假设。空假设是该模型符合所有预测器的假设。通常,显著性水平(用 α 或 alpha 表示)为 .05 即可。显著性水平 .0.05 指示当额外参数实际上不会显著改善分布拟合时,判定额外参数会显著改善分布拟合的风险为 5%。
如果 p 值小于或等于显著性水平,则可以得出数据不服从分布的结论。如果 P 值大于显著性水平,则无法得出模型解释响应中变异的结论。
- 阿哈斯情节
-
使用 Arjas 图确定该模型是否符合绝对预测器的相称危险假设。如果图中的曲线与 45 度线不同,则模型不符合预测器的相称危险假设。
如果模型不符合变量的假设,请尝试将变量用作分层变量。
- 安徒生情节
-
使用安徒生图来确定该模型是否符合不同地层的比例危险假设。一个或多个分层变量的每个值组合定义一个层。该图包含每个层的曲线。如果模型符合假设,则曲线是直线,穿过 X = 0 和 Y = 0 点。如果地层的基线危险率与 x 轴上的基线危险率相同,则曲线遵循图上的 45 度参考线。
如果模型不符合假设,请考虑是否将数据除以模型不符合比例危险假设的分层变量。然后对数据的每个子集进行单独的分析。单独的分析为每个子集中的预测器提供了不同的效果。
比率风险检验
| 项 | 自由度 | 相关 | 卡方 | P 值 |
|---|---|---|---|---|
| 年龄 | 1 | 0.1328 | 1.18 | 0.278 |
| 舞台 | ||||
| II | 1 | -0.0104 | 0.01 | 0.940 |
| III | 1 | -0.2445 | 2.86 | 0.091 |
| IV | 1 | -0.1193 | 0.63 | 0.426 |
| 整体 | 4 | — | 4.61 | 0.330 |
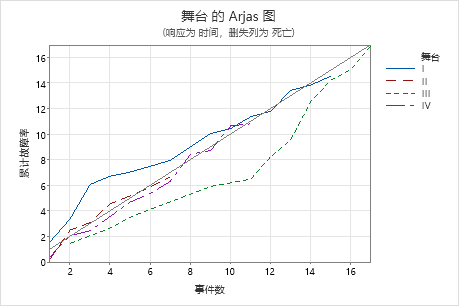
关键结果:P 值, 阿哈斯情节
在这些结果中,比例危险测试的 p 值均大于 0.05,因此您无法断定该模型不符合比例危险假设。
Arjas 图显示每个级别的累积危险率与事件数量 舞台。在这个 Arjas 情节中,线条通常遵循 45 度线,因此您可以得出结论,该模型符合预测器的相称危险假设 舞台。
