选择需要的方法或公式。
关于本主题
考虑两个有风险媒介的个体 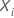 和
和 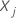 。个人的相对风险是个人风险的比例:
。个人的相对风险是个人风险的比例:
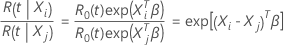
在考克斯比例危险模型中,比率的结果是恒定的。特别是,相对风险不取决于时间
t。 这个结果使得两个人的风险成正比。分类预测器的相对风险随之改变一个分类预测器之间的水平 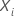 和
和 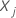 其他因子的符号保留不变。连续预测器的相对风险随后通过有意义的增量改变连续预测器的价值
其他因子的符号保留不变。连续预测器的相对风险随后通过有意义的增量改变连续预测器的价值
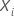 和
和 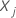 其他因子的符号保留不变。有关系数的计算及其标准错误的信息,请访问
系数和回归方程的方法和公式 以计数过程格式拟合 Cox 模型。
其他因子的符号保留不变。有关系数的计算及其标准错误的信息,请访问
系数和回归方程的方法和公式 以计数过程格式拟合 Cox 模型。
相对风险提供了回归系数的解释。对优势比的解释取决于预测变量是类别变量还是连续变量。
分类预测器的相对风险
对于绝对变量,相对风险表示将变量的某个级别的风险与变量另一级的风险进行比较。计算假定其他预测器的值保持不变。
设 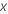 表示分类预测变量。两级
表示分类预测变量。两级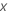 有以下代码:
有以下代码:
 和
和
 。设
。设
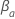 是回归系数
是回归系数  。设
。设
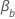 是系数
是系数  。比较的估计相对风险
(RR)
。比较的估计相对风险
(RR)  到
到
 具有以下形式:
具有以下形式:
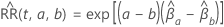
使用编码方案通过替换值来简化等式。 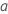 和
和
 ):
):
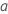 和
和
 ):
):
- 对于虚拟编码,
 和
和

- 对于效果编码,
 和
和

| 虚拟编码 (0, 1) | 效果编码 (-1, 0, 1) |
|---|---|
 |
 |
有了虚拟编码,参考级别始终具有系数 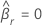 。
。
置信区间
100 (1 -  )
相对风险的信心区间有以下形式:
)
相对风险的信心区间有以下形式:
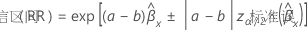
连续预测器的相对风险
设 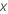 是连续预测器的观察值。计算假定其他预测器的值保持不变。连续预测器中的
c 单位变化具有以下相对风险:
是连续预测器的观察值。计算假定其他预测器的值保持不变。连续预测器中的
c 单位变化具有以下相对风险:
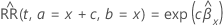
置信区间
100 (1 -  )
相对风险的信心区间有以下形式:
)
相对风险的信心区间有以下形式: