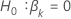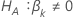回归方程
半参数考克斯比例危险模型使用个人的预测值, 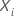 ,预测风险评分,
,预测风险评分, 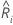 。回归方程的一般形式如下:
。回归方程的一般形式如下:

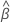 估计的系数的向量估计系数可以包括更高阶值的值,例如连续预测器的正方形。估计的风险评分适用于整个研究期间,不取决于时间。在输出中,方程有以下形式,其中不同级别的分类因子出现单独的方程:
估计的系数的向量估计系数可以包括更高阶值的值,例如连续预测器的正方形。估计的风险评分适用于整个研究期间,不取决于时间。在输出中,方程有以下形式,其中不同级别的分类因子出现单独的方程:
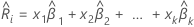
系数
让考克斯比例危险模型的日志部分可能性函数 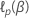 求逆。全模型可以最大化对数似然函数。
求逆。全模型可以最大化对数似然函数。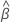 ,给出模型的估计系数。找到
,给出模型的估计系数。找到 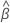 ,设置日志部分可能性函数的部分导数等于零,并解解方程
,设置日志部分可能性函数的部分导数等于零,并解解方程  。Minitab 统计软件使用牛顿-拉普森迭代方法来解解方程。见默里 (1972)1 牛顿-拉普森迭代方法的描述。
。Minitab 统计软件使用牛顿-拉普森迭代方法来解解方程。见默里 (1972)1 牛顿-拉普森迭代方法的描述。
日志部分可能性函数的部分衍生物的向量取决于响应变量是否包括绑定事件时间。如果响应变量包括领带,则估计使用 Efron 近似或布雷斯洛近似。如果响应变量没有联系,所有 3 种方法都提供相同的估计值。数据中的联系越少,两种近似方法的结果越接近。数据中的联系越多,Efron 近似度在布雷斯洛近似度上就越有改进。
| 项 | 说明 |
|---|---|
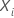 | 与事件时间对应的样本单位的共变值的载体 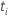 |
无领带数据
| 项 | 说明 |
|---|---|
 | 活动次数 |
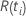 | 及时设置的风险 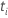 ,这是所有尚未在时间之前失败的样本单位的集 ,这是所有尚未在时间之前失败的样本单位的集 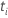 |
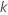 | “变量”是模型中的预测变量数。 哪里 哪里  是模型中的参数个数 是模型中的参数个数 |
考克斯比例危险模型的部分可能性函数没有联系,其形式如下:
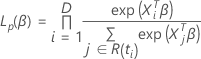
损失函数具有以下形式:
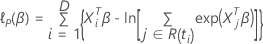
 具有以下形式:
具有以下形式:
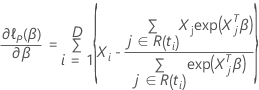
使特定系数的部分导数, 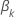 具有以下形式:
具有以下形式:
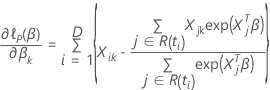
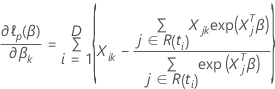
带领带的数据
| 项 | 说明 |
|---|---|
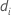 | 中的事件数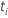 |
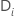 | 同时具有事件的所有示例单元集 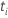 |
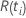 | 及时设置的风险 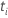 ,这是所有尚未在时间之前失败的样本单位的集 ,这是所有尚未在时间之前失败的样本单位的集 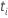 |

带领带的数据的 Efron 近似
损失函数具有以下形式:
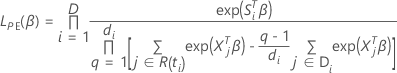
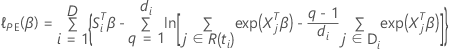
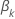 具有以下形式:
具有以下形式:
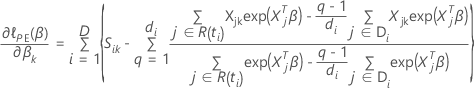
带领带的数据的布雷斯洛近似
损失函数具有以下形式:
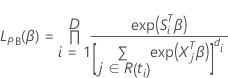
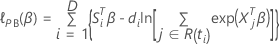
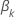 具有以下形式:
具有以下形式:
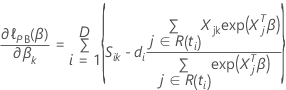
已编码系数
当分析标准化连续预测器时,表显示编码系数。要查找编码系数,请将标准化预测器替换为前方方程。
系数标准误
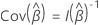
所观察到的信息矩阵,  取决于响应变量是否包括绑定事件时间。如果响应变量包括领带,则估计使用 Efron 近似或布雷斯洛近似。如果响应变量没有联系,所有 3 种方法都提供相同的估计值。数据中的联系越少,两种近似方法的结果越接近。数据中的联系越多,Efron 近似度在布雷斯洛近似度上就越有改进。
取决于响应变量是否包括绑定事件时间。如果响应变量包括领带,则估计使用 Efron 近似或布雷斯洛近似。如果响应变量没有联系,所有 3 种方法都提供相同的估计值。数据中的联系越少,两种近似方法的结果越接近。数据中的联系越多,Efron 近似度在布雷斯洛近似度上就越有改进。
无领带数据
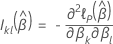
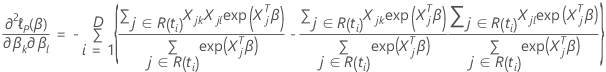
带领带的数据的 Efron 近似
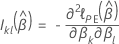
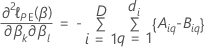
其中
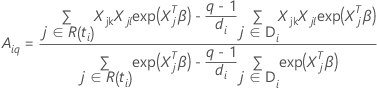
和
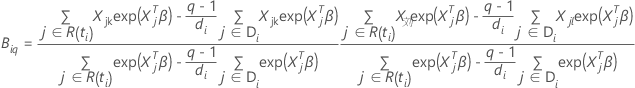
带领带的数据的布雷斯洛近似
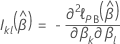
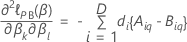
其中
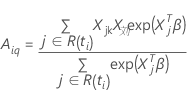
和
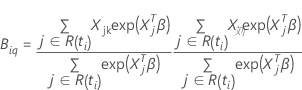
Z 值
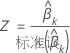
其中,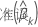 是系数的估计标准误差
是系数的估计标准误差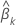 。价值
。价值 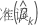 是 k对 角线元素的正方形根
是 k对 角线元素的正方形根  求逆。
求逆。
置信区间
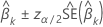
其中,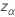 标准正态分布的上 α 百分位点
标准正态分布的上 α 百分位点
P 值

| 项 | 说明 |
|---|---|
 | 标准正态分布的随机变量 |
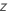 | 检验统计量(对于第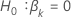 反对备择假设 反对备择假设 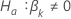 |
分层比例危险模型
对于包含以 s 水平为分层变量 的 分类变量的模型,整个地层的回归系数是恒定的。分层模型中回归系数的估计过程与不分层的比例危险模型的过程相同。对于分层模型,日志部分可能性函数具有以下形式:

其中,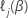 是地层 j中的日志部分可能性 。汇总每个层的衍生物,以获得部分可能性方程。每个层的衍生物与比例危险模型的衍生物相同,无需分层。Breslow 和 Efron 方法相应地适用。
是地层 j中的日志部分可能性 。汇总每个层的衍生物,以获得部分可能性方程。每个层的衍生物与比例危险模型的衍生物相同,无需分层。Breslow 和 Efron 方法相应地适用。