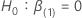方差分析提供了对模型中每个预测器统计意义的测试。
自由度
对优势比的解释取决于预测变量是类别变量还是连续变量。对于分类预测变量,自由度比预测变量 (k – 1) 中的水平数 k 小 1。对于一个连续的预测者,自由度总是1。对于一个较高的术语来说,自由度是综合术语自由度的产物。例如,两个三级分类预测器之间的交互自由度为 2 × 2 = 4。
卡方
- Wald 检验
- 似然比检验
- 分数测试
如果设计中存在聚类,则 Minitab 会根据 Wald 测试提供 ANOVA 表,因为可能性比和评分方法假定组集内的观测是独立的。
当响应变量没有绑定响应时间时,分数测试与众所周知的日志排名测试相同。
定义:
所有 3 种类型的测试的计算都使用以下定义。
设 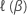 是布雷斯洛部分比勒功能或埃夫隆部分可能性功能评估 在β。
是布雷斯洛部分比勒功能或埃夫隆部分可能性功能评估 在β。
设 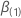 是一个
q组件载体和
是一个
q组件载体和 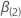 是一个(p -
q) 组件向量,以便 2 p 组分系数向量具有以下定义:
是一个(p -
q) 组件向量,以便 2 p 组分系数向量具有以下定义: 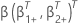 和
和 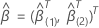
设 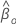 是
(部分) 最大可能性
是
(部分) 最大可能性  在限制模型下
在限制模型下
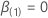 。然后,空假设下的最大可能性估计值具有以下形式:
。然后,空假设下的最大可能性估计值具有以下形式:
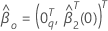
其中,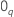 是零和的
q组分载体
是零和的
q组分载体  是
(部分) 最大可能性
是
(部分) 最大可能性 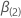 当
当 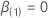 。
。
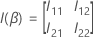
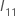 是以下
q ×
q 矩阵:
是以下
q ×
q 矩阵: 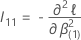
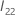 是以下
p •
q ×
p •
q 矩阵:
是以下
p •
q ×
p •
q 矩阵: 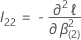
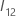 和
和  具有以下定义:
具有以下定义: 
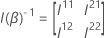
根据空假设,三个测试(Wald、可能性比和分数测试)中每个测试的测试统计具有无同位奇方分布, 具有 q 自由度。与模型中的参数数相比,观察到的事件数量大时,不对称分布是有效的。对于绝对预测器,每个级别的事件数量也必须足够大。
Wald 检验
对于 Wald 测试,测试统计具有以下形式:
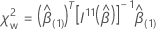
其中,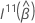 是上
q ×
q 子矩阵的
是上
q ×
q 子矩阵的  )。
)。
如果设计有集群,计算会利用来自林和伟(1989年)强力方差。1. 设
 是分数残余的矩阵。方差-协方差矩阵具有以下形式:
是分数残余的矩阵。方差-协方差矩阵具有以下形式:

其中,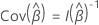 和
和
 是崩溃的分数剩余矩阵。要获取折叠的分数剩余矩阵,则以这些剩余行的总和替换每个分数残余行组。
是崩溃的分数剩余矩阵。要获取折叠的分数剩余矩阵,则以这些剩余行的总和替换每个分数残余行组。
似然比检验
对于似然比检验进行如下假设:
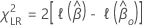
其中,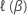 是适当的模型部分日志可能性函数。
是适当的模型部分日志可能性函数。
如果设计中存在聚类,则 Minitab 会根据 Wald 测试提供 ANOVA 表,因为可能性比和评分方法假定组集内的观测是独立的。
分数测试
设 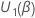 是日志可能性函数的部分导数的载体
是日志可能性函数的部分导数的载体
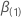 求逆。具体来说,此
q组件向量具有以下形式:
求逆。具体来说,此
q组件向量具有以下形式:
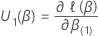
然后,分数测试的测试统计如下形式:
如果设计中存在聚类,则 Minitab 会根据 Wald 测试提供 ANOVA 表,因为可能性比和评分方法假定组集内的观测是独立的。
P 值
调整的 p 值具有以下表达式:
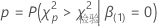
其中, 是一个随机变量, 遵循奇方分布与
是一个随机变量, 遵循奇方分布与  自由度。
自由度。 是检验统计量。
是检验统计量。