某可靠性工程师想要研究电子设备的晶体管之间的漏电情况。当漏电达到某个阈值时,电子设备会失效。为了加快检验的失效速度,检验设备的温度比正常温度高得多。每两天检查设备的失效情况。
工程师执行了加速寿命试验,以估计设备在正常操作条件 (55° C) 和最坏情况操作条件 (85° C) 下失效所需的时间。工程师想确定 B5 的寿命(5% 的设备失效所需的估计时间)。
- 打开样本数据,漏电.MWX。
- 选择。
- 选择响应为非删失/任意删失数据。
- 在变量/初始变量中,输入开始时间。
- 在结尾变量中,输入结束时间。
- 在频率列中,输入计数。
- 在加速变量中,输入温度。
- 从关系中,选择常规加速。
- 从假定分布中,选择Weibull。
- 单击估计。在百分位数和概率估计下面,选择输入新的预测变量值,然后输入新温度。
- 在估计下列百分比的百分位数中,输入 5,然后单击确定。
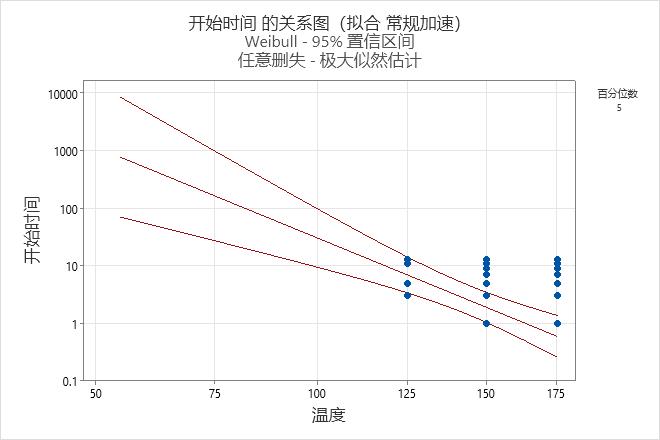
- 单击图形。在在图中要包括的设计值中,输入 55。
- 在关系图下面的绘制下列百分比的百分位数中,输入 5,然后选择在图中显示失效时间。
- 在每个对话框中单击确定。
解释结果
基于百分位数表中的结果,工程师可以断定以下结果:
- 在设计温度 (55°C) 下,5% 的设备将在大约 760 天(稍多于 2 年)后失效。
- 在最坏情况温度 (85°C) 下,5% 的设备将在大约 81 天之后失效。
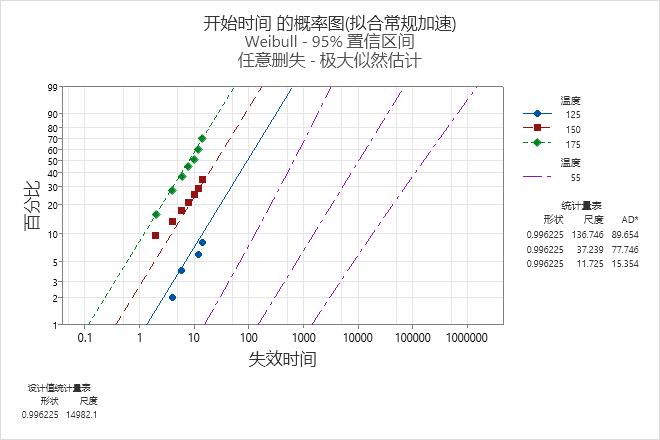
基于拟合模型的概率图可以帮助您确定加速变量每个水平的分布、变换以及相等形状假定 (Weibull) 是否合适。对于这些数据,点沿着近似的直线分布。因此,模型假定适合于加速变量水平。
响应变量初始:开始时间 结束: 结束时间
频率: 计数
删失
| 删失信息 | 计数 |
|---|---|
| 右删失值 | 95 |
| 区间删失值 | 58 |
估计法:极大似然
分布: Weibull
与加速变量的关系: 常规加速
回归表
| 95.0% 正态置信区间 | ||||||
|---|---|---|---|---|---|---|
| 自变量 | 系数 | 标准误 | Z | P | 下限 | 上限 |
| 截距 | -17.0990 | 4.13633 | -4.13 | 0.000 | -25.2061 | -8.99195 |
| 温度 | 0.755405 | 0.157076 | 4.81 | 0.000 | 0.447542 | 1.06327 |
| 形状 | 0.996225 | 0.136187 | 0.762071 | 1.30232 | ||
对数似然 = -191.130
百分位数表格
| 95.0% 正态置信区间 | |||||
|---|---|---|---|---|---|
| 百分比 | 温度 | 百分位数 | 标准误 | 下限 | 上限 |
| 5 | 55 | 759.882 | 928.717 | 69.2500 | 8338.21 |
| 5 | 85 | 81.0926 | 63.2317 | 17.5897 | 373.855 |