方差-协方差矩阵
Var (MLE) 和 Cov (μ,σ) 是 μ、σ、α 和 β(从 Fisher 信息矩阵的逆矩阵的相应单元提取)的 MLE 的方差和协方差。
正态分布、逻辑分布和最小极值分布的百分位数情况
估计百分位数 tp所需的样本量计算如下:
- 对于双侧置信区间:
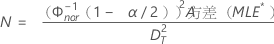
- 对于单侧置信区间:
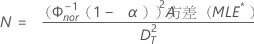
百分位数标准误差的计算
当分析规范包括样本数量时,分析将求解百分位数的标准误差。在本例中,以下公式给出了百分位数的渐近方差:
渐近方差(tp) = 渐近方差(MLE*)
表示法
- tp
- 百分位数
- MLE*
- tp的最大似然估计 (MLE)
- Avar(MLE*)
- 在设计(或使用)应力水平下,MLE 的渐近方差
- Φ-1正态分布
- 正态分布的逆 CDF
- DT
- 百分位数 (1–α)100% 置信区间宽度的一半
Weibull、指数分布、对数正态分布和对数逻辑分布的百分位数情况
估计百分位数 tp所需的样本量计算如下:
- 对于双侧置信区间:
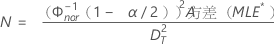
- 对于单侧置信区间:
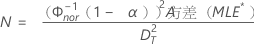


百分位数标准误差的计算
当分析规范包括样本数量时,分析将求解百分位数的标准误差。在本例中,以下公式给出了百分位数自然对数的渐近方差:
渐近方差 (tp) = (tp)2渐近方差(ln(tp))
表示法
| 项 | 说明 |
|---|---|
| tp | 百分位数 |
| MLE* | tp的最大似然估计 (MLE) |
| Avar(MLE*) | 在设计(或使用)应力水平下,MLE 的渐近方差 |
| Φ-1正态分布 | 正态分布的逆 CDF |
| D上部 | 估计值与上限之间的距离 |
| D下 | 估计值与下限之间的距离 |
可靠性案例
在估计可靠性时,标准化时间的 MLE 的计算公式如下:
- 对于双侧置信区间:
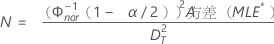
- 对于单侧置信区间:
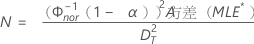
其中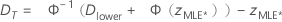

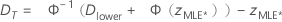

可靠性标准误差的计算
当分析规范包括样本数量时,分析求解可靠性的标准误差。在本例中,以下公式给出了可靠性的渐近方差:
Avar(可靠性) = (φ(zMLE*))2Avar(zMLE*)
其中 φ 的定义取决于分析的分布。
| 分布 | ϕ |
|---|---|
| 正常或对数正态 | 正态分布的 PDF |
| 逻辑或逻辑逻辑 | 物流分布的 PDF |
| Weibull、最小极值或指数 | 最小极值分布的 PDF |
表示法
| 项 | 说明 |
|---|---|
| MLE* | 标准化时间的最大似然估计 (MLE) (ZMLE*) |
| ZMLE* 表示正态分布、逻辑分布和最小极值分布 | 标准化时间 = (t − μ) / σ |
| ZMLE* 表示 Weibull、指数分布、对数正态分布和对数逻辑分布 | 标准化时间 = (ln(t) − μ) / σ |
| Avar(MLE*) | MLE 的渐近方差 |
| Φ-1正态分布 | 正态分布的逆 CDF |
| D上部 | 估计值与上限之间的距离 |
| D下 | 估计值与下限之间的距离 |
