可以使用优势比比较两个事件的几率。比率等于存在某个特定条件时的成功几率和存在另一个条件时的成功几率的比率。例如,您想比较接受家庭学校教育的学生与接受公共教育的学生。分析的目的是确定其中一组学生以优异成绩从大学毕业的几率是否更高一些。优势比构建如下:
- 家庭学校
-
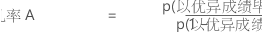
- 公立学校
-
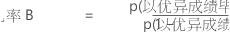
- 优势比
-

分母中的水平称为参考水平。在本示例中,公立学校是参考水平。如果此优势比等于 3.0,则接受家庭学校教育的学生以优异成绩毕业的几率是公立学校学生的 3 倍。
您可以通过选择 Logit 链接函数使用优势比。在 Logistic 回归中,优势比可用于比较类别响应变量每个水平的几率。比率将量化每个预测变量对每个响应水平的概率的影响。例如,假设您要确定年龄和性别是否会影响客户对混合动力车的选择。您用下列变量创建了一个 Logistic 回归模型:
| 变量 | 类型 | 说明 |
|---|---|---|
| 混合动力车 | 二元响应变量 | 客户不购买混合动力车时为 0,客户购买时为 1。 |
| 性别 | 二元预测变量 | 客户是男性时为 0,客户是女性时为 1。参考水平是男性。 |
| 年龄 | 连续预测变量 | 等于客户的年龄。可以等于任何非负值。 |
假设 Logistic 回归过程表明两个预测变量都很显著。如果性别的优势比为 2.0,女性购买混合动力车的几率是男性的两倍。如果年龄的优势比为 1.05,则客户的年龄每增加一岁,客户购买混合动力车的几率会增加 5%。
