有两种情况会阻止系数的极大似然估计值的收敛:完全分离和几乎完全分离。
完全分离
当预测变量的线性组合生成完美的响应变量预测时,会发生完全分离。例如,在下面的数据集中,如果 X ≤ 4,则 Y = 0。如果 X > 4,则 Y = 1。
| Y | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |
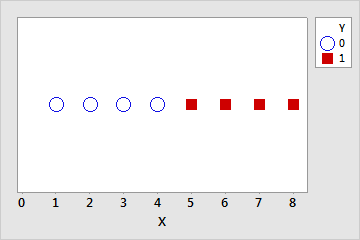
几乎完全分离
几乎完全分离与完全分离类似。预测变量可以为大多数(并非全部)预测变量值生成完美的响应变量预测。例如,在上一个数据集中,对于其中一个值,如果 X = 4,则让 Y = 1 而不是 0。现在,如果 X < 4,则 Y = 0;如果 X > 4,则 Y = 1;但如果 X = 4,则 Y 可能为 0 或 1。数据中间范围的重叠形成几乎完全分离。
| Y | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |

原因和纠正措施
通常情况下,当数据集太小而无法观测概率低的事件时,会发生分离。模型中的预测变量越多,就越可能发生分离,因为数据中的单个组的样本数量较小。
虽然 Minitab 会在发现分离时生成警告,但模型中的预测变量越多,发现产生分离的原因就越困难。模型中包含的交互作用项会加剧这一难度。
当极大似然估计值无法因分离而收敛时,请考虑以下 5 个策略:
- 增加数据量。分离通常发生在预测变量的类别或范围仅有一个响应值时。较大的样本数量会提高不同响应值的概率。
- 考虑分离的含义。当完全分离和几乎完全分离能够表示样本数量太小时,它们也可以表示重要的关系。如果在某个特定水平或水平组合的真实事件概率接近于 0 或 1,则此信息非常重要。
- 考虑备择模型。模型中的项越多,至少一个变量发生分离的概率越大。在为模型选择项时,可以检查排除某项时是否可以使极大似然估计收敛。如果存在不使用该项的有用模型,则可以使用此新模型继续执行分析。
- 检查是否可以合并问题变量的类别。如果存在适合合并的类别,则数据集中的分离可能会消失。例如,假设“水果”是模型中的一个变量。“葡萄柚”因试验数太少而不包含事件。将“葡萄柚”和“橘子”合并到“柑橘”类别中可消除分离。
表 : 1. 含有完全分离的数据 水果 事件数 试验数 葡萄柚 0 10 橘子 5 100 苹果 25 100 香蕉 40 100 表 : 2. 含有重叠的数据 水果 事件数 试验数 柑橘 5 110 苹果 25 100 香蕉 40 100 - 检查问题类别变量是否为综合变量。如果非综合变量与响应变量之间的关系未显示完全分离,则代入数字数可以消除分离。例如,假设“雇佣时间长度”是模型中的综合变量。当数据增量为 30 天时,最低水平包含所有事件,最高水平不包含任何事件,这会造成完全分离。将天数代入模型会消除分离。
表 : 3. 含有完全分离的数据 长度类别 事件数 试验数 1–90 2 2 91–180 1 2 181–270 1 2 271–360 0 2 确切长度 事件数 试验数 45 1 1 60 1 1 95 1 1 176 0 1 185 0 1 241 1 1 280 0 1 299 0 1
更多信息
有关分离的更多信息,请参考 Albert 和 J. A. Anderson (1984),“On the existence of maximum likelihood estimates in logistic regression models”(Logistic 回归模型中是否存在极大似然估计),Biometrika 第 71 卷,第 1 期,第 1–10 页。
