数据格式对二元 Logistic 回归中拟合优度的影响

对于二元 Logistic 回归，数据的格式会影响对偏差 R² 值和调整后偏差 R² 值的解释。在事件/试验格式中，每个观测值代表该行数据的所有试验中出现事件的概率。通常，此概率针对许多试验，而且介于 0 和 1 之间。与之相反，二元响应/频率格式中的每个观测值通常仅表示 1 个试验。单个试验的观测值为 1 或 0。

通常，数据格式之间的差异会使得数据中的总偏差不同。对于事件/试验数据，偏差与预测概率和观测概率之间的差异相关。对于二元响应/频率格式，偏差与预测概率和每个试验的结果（0% 或 100%）相关。事件/试验格式的数据中的偏差 R² 和调整后偏差 R² 通常较高。

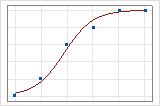
图示阐释了数据格式之间的差异。在这些图中，符号表示数据中的观测值，曲线表示模型中的预测值。对于事件/试验数据，符号接近直线。事件/试验数据的偏差 R² 值大约为 96%。模型能够很好地预测平均概率。

对于二元响应/频率数据，只有当直线接近 0% or 100% 时，观测值才接近预测直线。二元响应/频率数据的偏差 R² 值大约为 56%。预测概率和单个工况之间的关系不是那么强。

对于二元 Logistic 回归，数据的格式会影响偏差拟合优度检验是否可靠。偏差拟合优度检验的 p 值通常会随着每行试验数的递减而递减。二元响应/频率格式的数据中每行的试验数通常会较少。因此，如果数据为二元响应/频率格式，则偏差拟合优度检验可能指示拟合较差，即使实际上拟合很好也是如此。当数据为事件/试验格式，但每行的试验数较少时，偏差拟合优度检验还可能会错误地指出拟合较差。

Hosmer-Lemeshow 检验不依赖数据的格式。当数据中每行的试验数很少时，Hosmer-Lemeshow 检验能够更可靠地指出模型对数据的拟合优度。

比较相同数据在采用不同格式时的两组结果。对于这些数据，模型的形式是正确的。Hosmer-Lemeshow 检验的响应信息、系数和结果相同。偏差拟合优度检验的结论取决于数据格式。

在这些结果中，数据采用没有频率列的二元响应/频率格式。分析使用 500 行数据。每行表示 1 个试验。在 0.05 显著性水平下，偏差拟合优度检验的 p 值指示模型的拟合较差。此 p 值会导致错误地断定模型格式不正确。如果您收集二元响应/频率格式的数据，则偏差拟合优度检验通常不可靠。

在这些结果中，数据采用事件/试验格式。分析使用 5 行数据。每行数据表示 100 个试验。在 0.05 显著性水平下，偏差拟合优度检验的 p 值找不到差拟合模型的证据。如果您收集事件/试验格式的数据，偏差拟合优度检验通常比较可靠。

对于二元 Logistic 回归，数据的格式会影响 Pearson 拟合优度检验是否可靠。如果每行中的预计事件数量较小，则 Pearson 检验使用的卡方分布近似不准确。二元响应/频率格式的数据中每行的试验数通常会较少。因此，如果数据为二元响应/频率格式，则 Pearson 拟合优度检验可能不准确。

Hosmer-Lemeshow 检验不依赖数据的格式。当数据中每行的试验数很少时，Hosmer-Lemeshow 检验能够更可靠地指出模型对数据的拟合优度。

比较相同数据在采用不同格式时的两组结果。对于这些数据，模型的形式是正确的。实际模型包含 X1 和 X2 之间的交互作用。Hosmer-Lemeshow 检验的响应信息、系数和结果相同。Pearson 拟合优度检验的结论取决于数据格式。

在这些结果中，数据采用带有频率列的二元响应/频率格式。分析使用 18 行数据。每行表示 250 个 Bernoulli 试验。在 0.05 显著性水平下，Pearson 拟合优度检验的 p 值指示模型能够拟合数据。此 p 值会导致错误地断定模型足以拟合数据。如果您收集二元响应/频率格式的数据，则 Pearson 拟合优度检验不可靠。

在这些结果中，数据采用事件/试验格式。分析使用 9 行数据。每行数据表示 500 个试验。在 0.05 显著性水平下，Pearson 拟合优度检验的 p 值的确指出模型无法拟合数据。如果您收集事件/试验格式的数据，Pearson 拟合优度检验通常比较可靠。