具有一个固定批次因子和一个规格下限的模型的保质期
具有时间、批次和“时间*批次”交互作用项的模型
当模型中存在批次效应和“批次*时间”交互作用项时,第 i 个批次在时间 xij 的拟合值将使用遵循以下方程的模型:
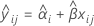
要确定保质期,请使以下方程等于规格下限并对时间 (x) 求解。
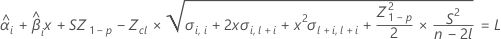
其中

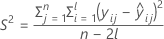
I = 批次水平总数
n = 响应值总数
X = 模型的设计矩阵
要计算有意义的保质期,Minitab 会评估三个条件。首先,Minitab 会确定在时间 = 0 时,均值响应在统计上是否大于规格下限。
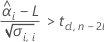
其次,Minitab 会确定均值响应是否会以统计上显著的速率随时间减小。

最后,Minitab 会确定二次方程的平方根部分是否有实数解。
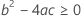
其中
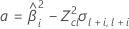
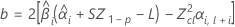
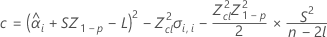
如果这三个条件都成立,则 Minitab 将计算保质期。要计算保质期,请使用二次方程。
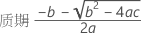
具有时间和批次的模型
当模型中不存在“批次*时间”交互作用项时,每个批次的斜率都相同。第 i 个批次在时间 xij 的拟合值将使用遵循以下方程的模型:
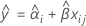
要确定保质期,请使以下方程等于规格下限并对时间 (x) 求解。
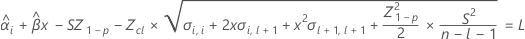
其中

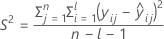
I = 批次水平总数
n = 响应值总数
X = 模型的设计矩阵
要计算有意义的保质期,Minitab 会评估三个条件。首先,Minitab 会确定在时间 = 0 时,均值响应在统计上是否大于规格下限。
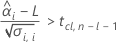
其次,Minitab 会确定均值响应是否会以统计上显著的速率随时间减小。
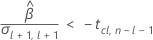
最后,Minitab 会确定二次方程的平方根部分是否有实数解。
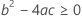
其中
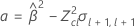

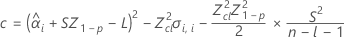
如果这三个条件都成立,则 Minitab 将计算保质期。要计算保质期,请使用二次方程。
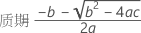
具有时间的模型
当模型中只存在时间时,每个批次的斜率和截距都相同。在时间 xij 处的拟合值将使用遵循以下方程的模型:
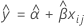
要确定保质期,请使以下方程等于规格下限并对时间 (x) 求解。
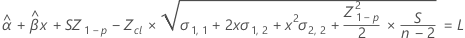
其中
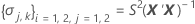
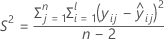
I = 批次水平总数
n = 响应值总数
X = 模型的设计矩阵
要计算有意义的保质期,Minitab 会评估三个条件。首先,Minitab 会确定在时间 = 0 时,均值响应是否大于规格下限。
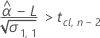
其次,Minitab 会确定均值响应是否会随时间减小。
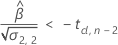
最后,Minitab 会确定二次方程的平方根部分是否有实数解。
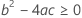
其中


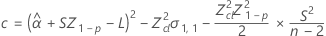
如果这三个条件都成立,则 Minitab 将计算保质期。要计算保质期,请使用二次方程。
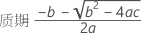
表示法
| 项 | 说明 |
|---|---|
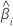 | 第 i 个批次的斜率 |
| Z | 给定概率的标准正态分布的逆累积概率函数的值 |
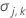 | 估计参数向量的方差 |
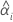 | 第 i 个批次的截距 |
| S2 | 均方误 |
| L | 规格下限 |
| X | 设计矩阵 |
| ii | 表示保质期估计值所在的批次的指数 |
| l | 批次因子中的水平数 |
| n | 响应值总数 |
具有一个固定批次因子和一个规格上限的模型的保质期
具有时间、批次和“时间*批次”交互作用项的模型
当模型中存在批次效应和“批次*时间”交互作用项时,第 i 个批次在时间 xij 的拟合值将使用遵循以下方程的模型:
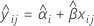
要确定保质期,请使以下方程等于规格上限并对时间 (x) 求解。
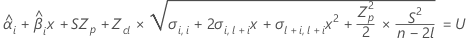
其中
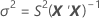
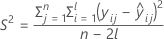
I = 批次水平总数
n = 响应值总数
X = 模型的设计矩阵
要计算有意义的保质期,Minitab 会评估三个条件。首先,Minitab 会确定在时间 = 0 时,均值响应在统计上是否小于规格上限。
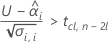
其次,Minitab 会确定均值响应是否会以统计上显著的速率随时间增大。
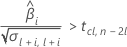
最后,Minitab 会确定二次方程的平方根部分是否有实数解。
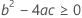
其中
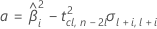

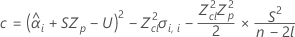
如果这三个条件都成立,则 Minitab 将计算保质期。要计算保质期,请使用二次方程。
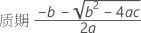
具有时间和批次的模型
当模型中不存在“批次*时间”交互作用项时,每个批次的斜率都相同。第 i 个批次在时间 xij 的拟合值将使用以下遵循以下方程的模型:
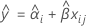
要确定保质期,请使以下方程等于规格上限并对时间 (x) 求解。
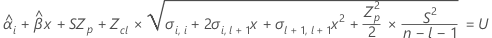
其中

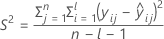
I = 批次水平总数
n = 响应值总数
X = 模型的设计矩阵
要计算有意义的保质期,Minitab 会评估三个条件。首先,Minitab 会确定在时间 = 0 时,均值响应在统计上是否小于规格上限。
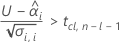
其次,Minitab 会确定均值响应是否会以统计上显著的速率随时间增大。
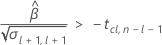
最后,Minitab 会确定二次方程的平方根部分是否有实数解。
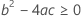
其中

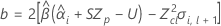
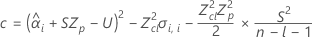
如果这三个条件都成立,则 Minitab 将计算保质期。要计算保质期,请使用二次方程。
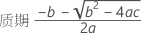
具有时间的模型
当模型中只存在时间时,每个批次的斜率和截距都相同。在时间 xij 处的拟合值将使用遵循以下方程的模型:
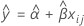
要确定保质期,请使以下方程等于规格上限并对时间 (x) 求解。

其中
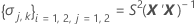
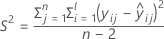
I = 批次水平总数
n = 响应值总数
X = 模型的设计矩阵
要计算有意义的保质期,Minitab 会评估三个条件。首先,Minitab 会确定在时间 = 0 时,均值响应是否小于规格上限。
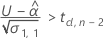
其次,Minitab 会确定均值响应是否会随时间增大。
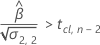
最后,Minitab 会确定二次方程的平方根部分是否有实数解。
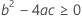
其中
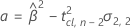

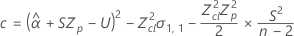
如果这三个条件都成立,则 Minitab 将计算保质期。要计算保质期,请使用二次方程。
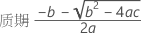
表示法
| 项 | 说明 |
|---|---|
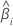 | 第 i 个批次的斜率 |
| Z | 给定概率的标准正态分布的逆累积概率函数的值 |
 | 估计参数向量的方差 |
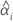 | 第 i 个批次的截距 |
| S2 | 均方误 |
| U | 规格上限 |
| X | 设计矩阵 |
| ii | 表示保质期估计值所在的批次的指数 |
| l | 批次因子中的水平数 |
| n | 响应值总数 |
两种规格限
要简化 Minitab 计算保质期的方式和时间的条件计算,请考虑要对数据拟合哪个模型。
具有时间、批次和“时间*批次”交互作用项的模型
要确定是否存在有意义的保质期估计值,Minitab 会评估两个条件。首先,Minitab 会确定均值响应在统计上是否位于规格限内。
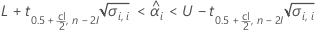
其中

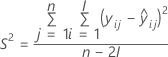
| 项 | 说明 |
|---|---|
| I | 批次水平总数 |
| n | 响应值总数 |
| X | 模型的设计矩阵 |
其次,Minitab 会确定均值响应是否会以统计上显著的速率随时间变化。
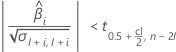
如果存在有意义的估计值,Minitab 会确定均值响应随时间增大还是减小。如果第二个条件不成立,则以下条件之一成立。
如果响应随时间减小,Minitab 将计算相对于规格下限的保质期。当响应减小时,以下公式可以满足该条件:
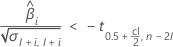
如果响应随时间增大,Minitab 将计算相对于规格上限的保质期。当响应增大时,以下公式可以满足该条件:
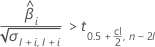
如果均值响应随时间减小,Minitab 将计算相对于规格下限的保质期。否则,Minitab 将计算相对于规格上限的保质期。
有关为每个案例计算保质期的详细信息,请转到对应的主题:
具有时间和批次的模型
要确定是否存在有意义的保质期估计值,Minitab 会评估两个条件。首先,Minitab 会确定均值响应在统计上是否位于规格限内。
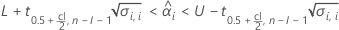
其中

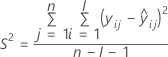
| 项 | 说明 |
|---|---|
| I | 批次水平总数 |
| n | 响应值总数 |
| X | 模型的设计矩阵 |
其次,Minitab 会确定均值响应是否会以统计上显著的速率随时间变化。
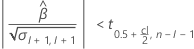
如果存在有意义的估计值,Minitab 将确定是估计相对于规格上限的保质期还是相对于规格下限的保质期。
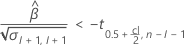
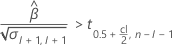
有关为每个案例计算保质期的详细信息,请转到对应的主题:
具有时间的模型
要确定是否存在有意义的保质期估计值,Minitab 会评估两个条件。首先,Minitab 会确定均值响应在统计上是否位于规格限内。
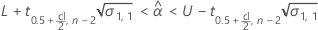
其中

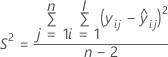
| 项 | 说明 |
|---|---|
| I | 批次水平总数 |
| n | 响应值总数 |
| X | 模型的设计矩阵 |
其次,Minitab 会确定均值响应是否会以统计上显著的速率随时间变化。
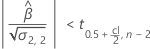
如果存在有意义的估计值,Minitab 将确定是估计相对于规格上限的保质期还是相对于规格下限的保质期。
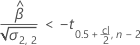
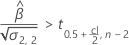
有关为每个案例计算保质期的详细信息,请转到对应的主题:
表示法
| 项 | 说明 |
|---|---|
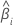 | 第 i 个批次的斜率 |
| I | 批次因子中的水平数 |
| n | 数据中的行数 |
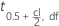 | 具有自由度 (DF) 的 t 分布的逆累积分布函数在 0.5+cl/2 处的值 |
