混合模型和对数似然
混合模型的一般形式
混合效应模型包含固定效应和随机效应。混合效应模型的一般形式为:
y = Xβ + Z1μ1+ Z2μ2 + ... + Zcμc + ε
表示法
| 项 | 说明 |
|---|---|
| y | 响应值的 n x 1 向量 |
| X | 固定效应的 n x p 设计矩阵,p ≤ n |
| Zi | 模型中第 i 个随机效应的 n x mi 设计矩阵 |
| β | 未知参数的 p x 1 向量 |
| μi | N(0, σ2i) 中的自变量的 mi x 1 向量 |
| ε | N(0, σ2i) 中的自变量的 n x 1 向量 |
| c | 模型中的随机效应数 |
固定模型的特定形式
稳定性研究拟合两个具有一个随机批次因子的模型。最大的模型包含时间、随机批次因子以及时间和批次之间的随机交互作用项。
y = Xβ + Z1μ1+ Z2μ2 + ε
最小的模型包含时间和随机批次因子。
y = Xβ + Z1μ1+ε
响应向量 y 的一般方差-协方差矩阵为:
V(σ2) = V(σ2, σ21, ... , σ2c) = σ2In + σ21Z1Z'1 + ... + σ2cZcZ'c
其中
σ2 = (σ2, σ21, ... , σ2c)'
σ2, σ21, ... , σ2c are called variance components.
通过分解方差,您可以在计算混合模型的对数似然时找到 H(θ) 的表示形式。
V(σ2) = σ2H(θ) = σ2[In + θ1Z1Z'1 + ... + θcZcZ'c]
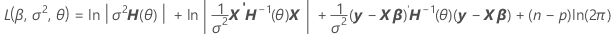
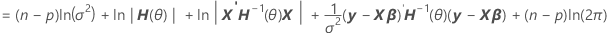
表示法
| 项 | 说明 |
|---|---|
| n | 观测值个数 |
| p | β 中的参数个数,稳定性研究有 2 个参数 |
| σ2 | 误差方差分量 |
| X | 设计矩阵 –– 对于固定项、常量和时间 |
| H(θ) | In + θ1Z1Z'1 + ... + θcZcZ'c |
| In | 具有 n 个行和列的恒等矩阵 |
| θi | 第 i 个随机项的方差与误差方差的比率 |
| Zi | 模型中第 i 个随机效应的已知编码的 n x mi 矩阵 |
| mi | 第 i 个随机效应的水平数 |
| c | 模型中的随机效应数 |
| |H(θ)| | H(θ) 的行列式 |
| X' | X 的转置 |
| H-1(θ) | 逆 H(θ) |
Box-Cox 变换
Box-Cox 变换选择能够最小化残差平方和的 lambda 值(如下所示)。由此生成的变换是 Yλ(当 λ ≠ 0 时)及 ln(Y)(当 λ = 0 时)。当 λ < 0 时,Minitab 还会将变换后响应乘以 −1,以维持未变换响应的顺序。
Minitab 搜索介于 −2 和 2 之间的最优值。此区间以外的值生成的拟合可能较差。
以下是一些常见的变换,其中 Y' 是数据 Y 的变换:
| Lambda (λ) 值 | 变换 |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = .5 | Y′ = 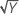 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −.5 |  |
| λ = −1 | Y′ = −1 / Y |
随机批次模型选择
- 时间 + 批次 + 批次*时间(批次的斜率和截距都不相等)
- 时间 + 批次(批次的斜率相等,截距不相等)
- 时间(批次的斜率和截距都相等)
如果“批次*时间”交互作用项显著,则该分析将拟合第一个模型。如果交互作用项不显著,但批次项在第二个模型中显著,则该分析将拟合第二个模型。否则,该模型将拟合第三个模型。
是否合并批次的检验与包括批次的检验略有不同,尽管这两种检验都取决于卡方分布。检验统计量和 P 值的公式如下所示。
模型 1 和模型 2 之间的检验
差分 = −2L2 − (−2L1)
p = 0.5 * Prob(χ21 > 差分) + 0.5 * Prob(χ22 > 差分)
模型 2 和模型 3 之间的检验
差分 = −2L3 − (−2L2)
p = 0.5 * Prob(χ21 > 差分)
表示法
| 项 | 说明 |
|---|---|
| La | 模型 a 的对数似然 |
| p | 检验的 p 值 |
| Prob(χ21> 差分) | 自由度为 1 的卡方分布中的随机变量的概率大于差分 |
| Prob(χ22> 差分) | 自由度为 2 的卡方分布中的随机变量的概率大于差分 |
参考资料
- Searle S.R.、Casella G. 和 McCuloch C.E. (1992)。Variance Components(方差分量)
- West B.T.、Welch K.B. 和 Galecki A.T. (2007)。Linear Mixed Models: A Practical Guide Using Statistical Software(线性混合模型:使用统计软件的实用指南)。
- Chow S. (2007)。Statistical Design and Analysis of Stability Studies(稳定性研究的统计设计和分析)。
