请选择您所选的方法或公式。
拟合值
预测的 Y 或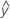 
；使用估计回归方程的给定预测变量值的平均响应值。
边际拟合值的标准误 (SE Fit)
混合模型中边际拟合值的标准误取决于固定效应的检验方法。对于两种方法，标准误是拟合值方差矩阵的对角线元素的平方根。
Kenward-Roger 法
其中
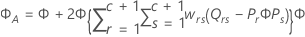
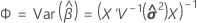
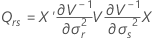
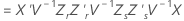
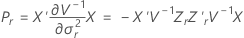
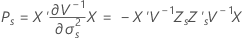
Satterthwaites 近似
其中
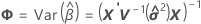
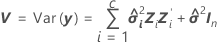
残差
残差是观测值与拟合值之间的差分。拟合模型不解释这部分观测值。观测值的残差为：
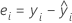
当批次是随机因子时，Minitab 会计算 2 种类型的残差。边际残差使用随机批次的拟合值，因此该方程中不存在批次的系数。
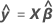
条件残差使用数据中某个批次的拟合值。
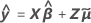
表示法
| 项 | 说明 |
|---|---|
| yi | 第 i 个观测响应值 |
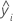 | 第 i 个拟合响应值 |
 | 拟合响应的向量 |
| X | 固定效应的设计矩阵 |
 | 固定预测变量的向量 |
| Z | 随机因子的设计矩阵 |
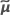 | 估计的 BLUP 值的向量 |
标准化残差
标准化残差又称“内部标准化残差”。
其中，残差的标准差是残差方差矩阵相应的对角线平方根：
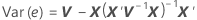
其中
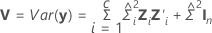
表示法
| 项 | 说明 |
|---|---|
| ei | 第 i 个残差 |
| Std(ei) | 第 i 个残差的标准差 |
置信区间
一组给定预测变量值的估计均值响应将落入的范围。
混合模型中拟合值的标准误是此矩阵的对角线元素的平方根：
其中
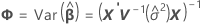
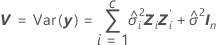
当批次是随机因子时，自由度将使用以下公式：
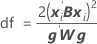
其中
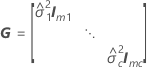
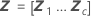
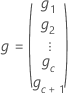
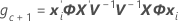
表示法
| 项 | 说明 |
|---|---|
| t1-α/2, df | 具有给定自由度的 t 分布的 1–α/2 分位数 |
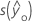 | 拟合值的标准误 |
| X | 设计矩阵，包括常量 |
| X' | X 的转置 |
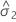 | 误差方差分量 |
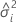 | 第 i 个随机因子的方差分量 |
| Zi | 模型中第 i 个随机效应的已知编码的 n x mi 矩阵 |
| Zi' | Zi 的转置 |
| In | 具有 n 个行和列的恒等矩阵 |
| xi | 拟合或预测的预测变量值 |
| W | 误差方差分量的渐近方差-协方差矩阵 |
| c | 模型中的随机效应数 |
预测区间
一个新观测值的预测响应将落入的范围。预测区间的计算取决于是要计算边际拟合的区间还是条件拟合的区间。
边际拟合
其中
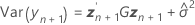
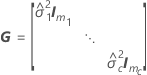
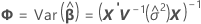
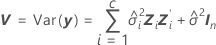
以下公式可以指定 t 统计量的自由度：
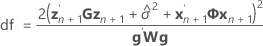
其中
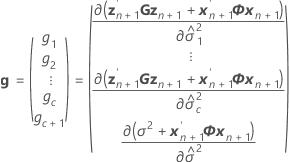
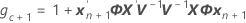
条件拟合
其中
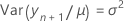
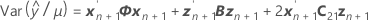
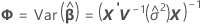
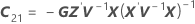
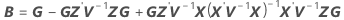
t 统计量的自由度为：
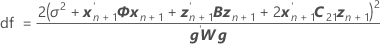
其中
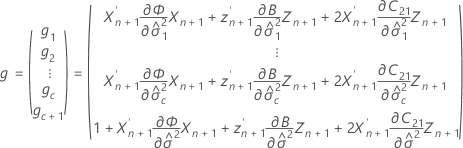
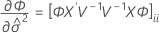
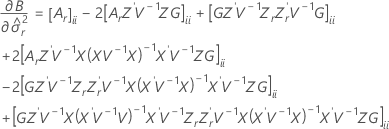
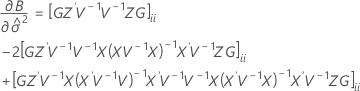
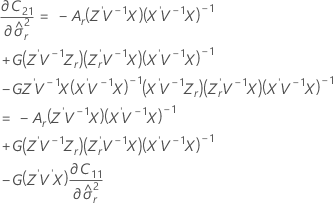
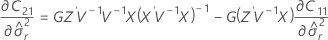
表示法
| 项 | 说明 |
|---|---|
 | 具有给定自由度的 t 分布的 1–α/2 百分位数 |
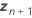 | 新随机预测变量值的向量 |
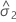 | 误差方差分量 |
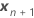 | 新固定预测变量值的向量 |
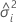 | 第 i 个随机因子的方差分量 |
| Im | 具有 m 个行和列的恒等矩阵 |
| m | 可表示模型中第 i 个随机项的设计矩阵中的列数 |
| c | 模型中的随机效应数 |
| Zi | 模型中第 i 个随机效应的 n x mi 设计矩阵 |
| Z'i | Zi 的转置 |
