步骤 1:确定响应变量和项之间的关联在统计上是否显著
如果数据包括批次因子,则模型选择表将显示模型选择过程的结果。Minitab 使用选择过程中的最终模型估计保质期。
Minitab 会从包括时间、批次和“批次*时间”交互作用项的全模型开始。然后,Minitab 会将交互作用项的 P 值与在合并批次的 Alpha中指定的值(又称 α)进行比较。如果交互作用项的 P 值小于 α,则无法简化模型。最终模型将包括所有这三项。
如果交互作用项的 P 值大于或等于 α,则 Minitab 会删除该交互作用项并评估只包含时间和批次的简化模型。如果简化模型中批次的 P 值小于 α,则无法进一步简化该模型。最终模型将包括时间和批次。
如果简化模型中批次的 P 值大于或等于 α,则 Minitab 将删除批次。最终模型将只包括时间。
模型选择,α = 0.25
| 来源 | 自由度 | Seq SS | Seq MS | F 值 | P 值 |
|---|---|---|---|---|---|
| 月数 | 1 | 122.460 | 122.460 | 345.93 | 0.000 |
| 批次 | 4 | 2.587 | 0.647 | 1.83 | 0.150 |
| 月数*批次 | 4 | 3.850 | 0.962 | 2.72 | 0.048 |
| 误差 | 30 | 10.620 | 0.354 | ||
| 合计 | 39 | 139.516 |
主要结果:P 值
在这个包含固定批次因子的示例中,“月份*批次”交互作用项的 P 值为 0.048。由于 P 值小于显著性水平 0.25,因此每个批次的回归方程中的斜率都不同。
步骤 2:确定产品的保质期
保质期估计表显示规格限、用于计算保质期的置信水平以及保质期估计值。
如果批次因子是固定因子,并且最终模型不包括该批次因子,则所有批次的保质期都相同。否则,每个批次的保质期都不同,并且 Minitab 会显示每个批次的保质期估计值。产品的整体保质期等于各个保质期的值中的最小值。
如果批次因子是随机因子,则 Minitab 只会计算整体保质期。
估计稳定期
稳定期 = 您可以 95% 确信至少 50% 的响应高于规格下限的时间期间
| 批次 | 稳定期 |
|---|---|
| 1 | 83.552 |
| 2 | 54.790 |
| 3 | 57.492 |
| 4 | 60.898 |
| 5 | 66.854 |
| 整体 | 54.790 |
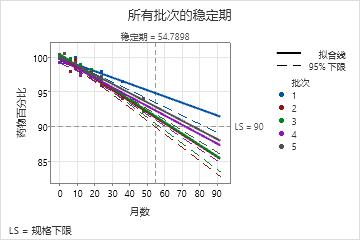
主要结果:保质期估计值、保质期图
在这些结果中,最终模型包括批次因子,因此 Minitab 会显示每个批次的保质期估计值。整体保质期估计值为 54.79 个月。该值是批次 2(保质期最短)的保质期。
步骤 3:检查项如何与响应关联
对于固定批次因子,如果时间是最终模型中的唯一一个项,则所有批次都将共享相同的截距和斜率,而且 Minitab 会显示一个回归方程。否则,Minitab 会为每个批次显示一个单独的方程。如果最终模型包括批次因子但不包括“批次*时间”交互作用项,则所有批次的截距都不同但降级速率相同。如果最终模型包括批次项和“批次*时间”交互作用项,则所有批次的截距和斜率都不同。
回归方程
| 批次 | |||
|---|---|---|---|
| 1 | 药物百分比 | = | 99.853 - 0.0909 月数 |
| 2 | 药物百分比 | = | 100.153 - 0.1605 月数 |
| 3 | 药物百分比 | = | 100.479 - 0.1630 月数 |
| 4 | 药物百分比 | = | 99.769 - 0.1350 月数 |
| 5 | 药物百分比 | = | 100.173 - 0.1323 月数 |
主要结果:回归方程
在这些结果中,月份和“月份*批次”交互作用项显著。因此,每个批次的回归方程都具有不同的截距和斜率。批次 3 具有最大斜率 −0.1630,这表示批次 3 的药物浓度(药物 %)每个月会降低 0.163 个百分点。批次 4 具有最小截距 99.769,这表示批次 4 在时间为零时浓度最低。
步骤 4:确定模型对数据的拟合优度
要确定模型与数据的拟合优度,请检查模型汇总表中的拟合优度统计量。
- R-sq
-
R2 是由模型解释的响应中的变异百分比。R2 值越高,模型拟合数据的优度越高。R2 始终介于 0% 和 100% 之间。
如果向模型添加其他预测变量,则 R2 会始终增加。例如,最佳的 5 预测变量模型的 R2 始终比最佳的 4 预测变量模型的高。因此,比较相同大小的模型时 R2 最有效。
- R-Sq(调整)
-
在想要比较具有不同数量的预测变量的情况下,使用调整的 R2。如果向模型添加预测变量,即使模型没有实际改善,R2 也会始终增加。调整的 R2 值包含模型中的预测变量数,以便帮助您选择正确的模型。
-
样本数量较小则不能提供对于响应变量和预测变量之间关系强度的精确估计。如果需要 R2 更为精确,则应当使用较大的样本(通常为 40 或更多)。
-
拟合优度统计量只是模型拟合数据优度的一种度量。即使模型具有合意的值,您也应当检查残差图,以验证模型是否符合模型假设。
模型汇总
| S | R-sq | R-sq(调整) | R-sq(预测) |
|---|---|---|---|
| 0.594983 | 92.39% | 90.10% | 85.22% |
主要结果:R-sq
在这些结果中,R2 和调整的 R2 都接近于 100,这表示模型可以很好地拟合数据。
步骤 5:确定模型是否符合分析的假设条件
使用残差图可帮助您确定模型是否适用并符合分析的假设。如果不符合此假设,则模型可能无法充分拟合数据,在解释结果时应当格外小心。
注意
如果模型中包括随机批次因子,可以绘制边际和条件残差。边际拟合值是整个总体的拟合值。使用条件残差可以检查模型中误差项的正态性。
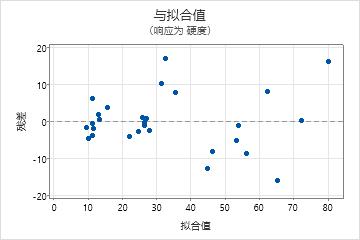
残差与拟合值图
使用残差与拟合值图可验证残差随机分布和具有常量方差的假设。理想情况下,点应当在 0 的两端随机分布,点中无可辨识的模式。
| 模式 | 模式的含义 |
|---|---|
| 残差相对拟合值呈扇形或不均匀分散 | 异方差 |
| 曲线 | 缺少高阶项 |
| 远离 0 的点 | 异常值 |
| 在 X 方向远离其他点的点 | 有影响的点 |
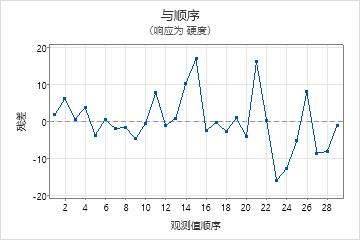
残差与顺序图
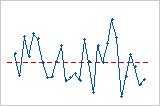
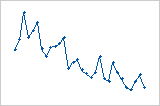
趋势
偏移
周期
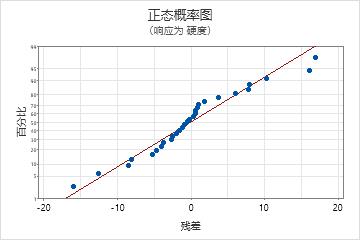
正态概率图
使用残差正态概率图可验证残差呈正态分布的假设。残差的正态概率图应该大致为一条直线。
| 模式 | 模式的含义 |
|---|---|
| 非直线 | 非正态性 |
| 远离直线的点 | 异常值 |
| 斜率不断变化 | 未确定的变量 |
有关如何处理残差图模式的更多信息,请转到拟合线图的残差图。
