残差的直方图
残差的直方图显示所有观测值的残差分布。
解释
| 模式 | 模式的含义 |
|---|---|
| 一个方向的长尾 | 偏度 |
| 远离其他条形的条形 | 异常值 |
因为直方图的外观取决于用来进行数据分组的区间数,所以请勿使用直方图评估残差的正态性。反之,可使用正态概率图。
在具有大约 20 个或更多个数据点时,直方图效果最明显。如果样本过小,则直方图的每个条形未包含可靠显示偏度或异常值的足够数据点。
残差的正态概率图
残差的正态概率图显示,当分布呈正态时,残差与期望值的关系。
注意
如果批次因子是随机因子,则使用条件残差来评估正态性。
解释
使用残差正态概率图可验证残差呈正态分布的假设。残差的正态概率图应该大致为一条直线。
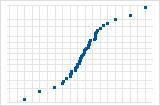
S 曲线表示长尾分布。
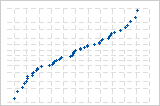
反向 S 曲线表示短尾分布。
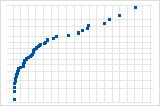
向下的曲线表示右偏斜分布。
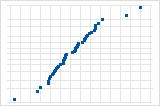
远离线的几个点表示分布中有异常值。
如果发现非正态模式,则使用其他残差图检查该模型是否存在其他问题,例如,异方差或时间顺序效应。如果残差不遵循正态分布,且数据中的观测值少于 15 个,则预测的置信区间、系数的置信区间以及系数的 P 值可能不准确。
残差与拟合值

含异常值的图
其中一个点比所有其他点大得多。因此,该点是异常值。如果异常值过多,则模型可能不可接受。您应该尝试找出导致任何异常值的原因。更正任何数据输入错误或测量误差。考虑删除与异常的单次事件(也称为特殊原因)相关联的数据值。然后,重新执行分析。
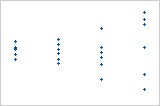
含异方差的图
残差的方差随拟合值增加。请注意,随着拟合值增大,残差之间的散布变宽。此模式表示残差的方差不相等(非恒定)。
如果要确定残差与拟合值图中的任何模式或异常值,请考虑使用以下解决方案:
| 问题 | 可能解决方案 |
|---|---|
| 异方差 | 考虑使用 Box-Cox 变换。有关更多信息,请转到为稳定性研究执行 Box-Cox 变换。 |
| 异常值或有影响的点 |
|
残差与顺序
残差与顺序图按照数据的收集顺序显示残差。
解释
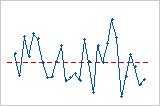
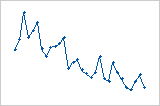
趋势
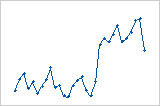
偏移
周期
残差与变量
残差与变量的关系图显示残差与另一个变量的关系。已在模型中包含此变量。或者,模型中未包含此变量,但是猜测它会影响响应。
解释
如果在残差中看到非随机图形,则表明变量会系统性地影响响应。请考虑在分析中包含此变量。
